
Десь там на числовому ряді зачаїлися величезні прості числа, зачаїлися і чекають, коли їх виявлять. Минулої середи знайшли нове. The Great Internet Mersenne Prime Search [Великий інтернет-пошук простих чисел Мерсенна], організація, присвячена робити власне те, що заповідає його назва, оголосила, що виявила нове просте число, найбільше з коли-небудь знайдених: 2⁷⁷²³²⁹¹⁷-1. Це понад 77 мільйонів двійок, перемножених між собою, і мінус 1. Я би написав його для вас, але є велика проблема: це 23 249 425 цифр [майже 13 тис. аркушів тексту, — Z] (зате воно має своє ім'я: M77232917.)
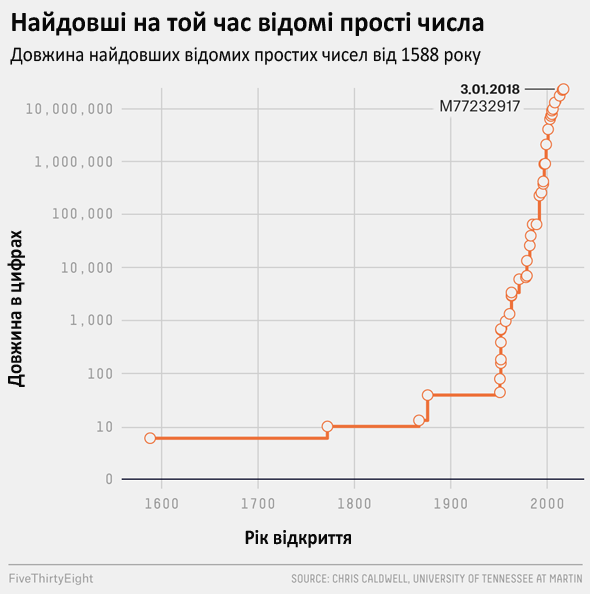
Замість того, щоб виписувати його, я пропоную оцю діаграму, що показує, як з часом змінювалась довжина найдовшого відомого простого числа. (Ми подали діаграму в логарифмічній шкалі, щоб можна було легко порівняти величезний діапазон чисел.)
Просте число — це число, яке ділиться тільки на себе і на одиницю. Ці числа грають важливу роль в чистій математиці та її розділі теорії чисел. Тут наголос на слові "чиста". Британський математик Ґ. Г. Гарді якось з гордістю написав, що теорія чисел настільки вільна від практичного застосування, що "ніхто ще не виявив жодних військових цілей, яким має служити теорія чисел". (Що, однак, останнім часом змінилося, бо тепер прості числа відіграють важливу роль в криптографії.)
Математики довго шукали прості числа протягом століть, часто послуговуючись лиш пером та мозком. В 1588 році італійський математик довів, що 524287, або 2¹⁹-1, є просте. В 1772 році легендарний Леонард Ейлер показав, що 2147483647, або 2³¹-1, теж просте.
Потім з'явився комп'ютер. Сходження зорі комп'ютерної ери ви можете чітко побачити в наведеній вище діаграмі. Протягом останніх приблизно 70 років найдовші відомі прості числа ставали в тисячі і тисячі разів більшими. Суперкомп'ютери стали манною небесною для мисливців за простими числами. Відкриття більших простих чисел йшли разом з розвитком швидших і потужніших процесорів.
Нині проект Great Internet Mersenne Prime Search полювання на своїх мамонтів базує на розподілених обчисленнях. Як і в аналогічних проектах для згортання білків і пошуку космітів, добровольці завантажують програми для пошуку простих чисел і жертвують для проекту свої вільні обчислювальні потужності. Один з таких добровольців, Джонатан Пейс, і відкрив на своєму комп'ютері M77232917 в день після Різдва. Він шукав його 14 років. Знадобилося ще шість днів, щоб довести, що число дійсно просте.
M77232917, звичайно, не є найбільшим простим числом. Фактично, нема найбільшого простого числа. Їх є нескінченно багато — цей факт був встановлений грецьким математиком Евклідом близько 300 р. до н. е. Залишаються фасцинуючі відкриті питання про прості числа, наприклад, гіпотеза Гольдбаха (що цікавиться, чи можна кожне парне ціле число більше 2 виразити сумою двох простих чисел) чи гіпотеза про прості числа-близнюки (що цікавиться, чи існує нескінченна кількість пар простих чисел, різниця між якими становить 2 — таких як 11 і 13).
Але знаходження все більших і більших простих чисел не доводить цих математичних ідей. То нащо полювати? Резони, пропоновані головним пошуковим проектом, включають традицію, колекцію, славу і гроші. Передбачено приз $250,000 за перше мільярд-значне просте число. Щасливого полювання.
Oliver Roeder
We Have A New Prime Number, And It’s 23 Million Digits Long
FiveThirtyEight, 5.01.2018
Переклад О.Д.
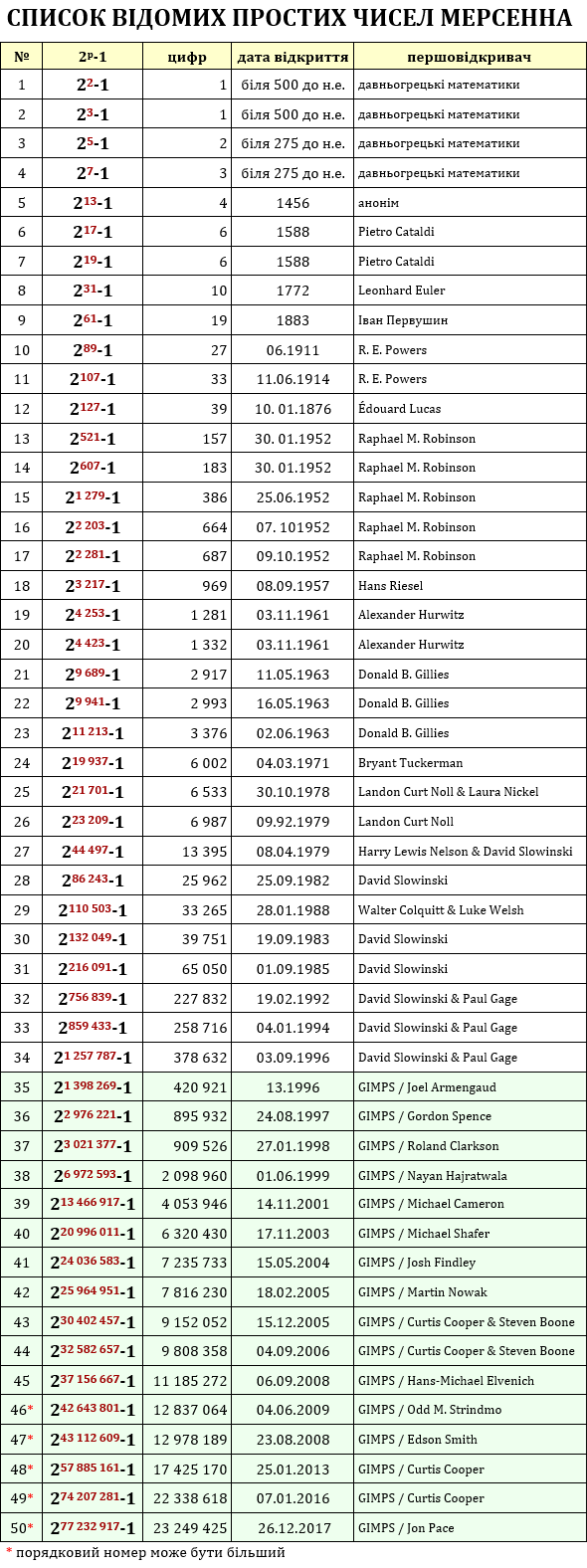 Джерело: mersenne.org
Джерело: mersenne.org
