Про математику. Від основ до незбагненного.

Найбільш відомі ідеї геометрії були навіяні античним баченням — баченням світу плоским. Від паралельних ліній, які ніколи не перетинаються, до Піфагорової теореми, про яку ми вже говорили, — такими є вічні істини про уявне місце, двовимірний простір плоскої геометрії.
Зароджена в Індії, Китаї, Єгипті і Вавилонії понад 2,5 тис. років тому й систематизована та вдосконалена Евклідом і стародавніми греками, ця геометрія плоскої землі є основною (і часто єдиною), якої навчають нині у середній школі. Та за кілька тисячоліть, що минули, дещо змінилося.
В епоху ґлобалізації, Google Earth і трансконтинентальних повітряних подорожей кожен з нас мусить спробувати бодай трохи дізнатися про сферичну геометрію та її сучасне узагальнення — диференціальну геометрію. Її основним ідеям лише 200 років. Заснована Карлом Фрідріхом Гаусом і Бернгардом Ріманом, диференціальна геометрія підпирає такі вражаючі інтелектуальні споруди, як загальна теорія відносності Ейнштейна. Проте в її основі лежать прекрасні ідеї, які може збагнути кожен, хто колись їздив на ровері, дивився на ґлобус чи розтягував ґумову стрічку. І їхнє розуміння допоможе вам зрозуміти кілька цікавинок, які ви могли зауважити під час ваших мандрівок.
Наприклад, коли я був маленьким, мій тато полюбляв перевіряти, як я знаю географію. Що лежить північніше — Рим чи Нью-Йорк, запитував він. Більшість людей сказали би, що Нью-Йорк, але, як це не дивно, вони є майже на тій самій широті, Рим трохи північніше. На звичайній мапі світу (оманливій проекції Меркатора, де Гренландія видається гігантською) виглядає так, що ви можете мандрувати з Нью-Йорка безпосередньо до Рима, взявши курс прямо на схід.
Проте пілоти авіаліній ніколи не обирають такого маршруту. Вилітаючи з Нью-Йорка, вони завжди беруть курс на північний схід, тримаючись узбережжя Канади. Колись я думав, що вони тримаються близько землі заради безпеки, але не це є причиною. Це попросту найпряміший маршрут, якщо ви врахуєте кривину Землі. Найкоротший шлях з Нью-Йорка до Рима пролягає через Нову Шотландію і Ньюфаундленд, потім над Атлантикою, й нарешті повертає на південь Ірландії, через Францію, щоби прибути до сонячної Італії.
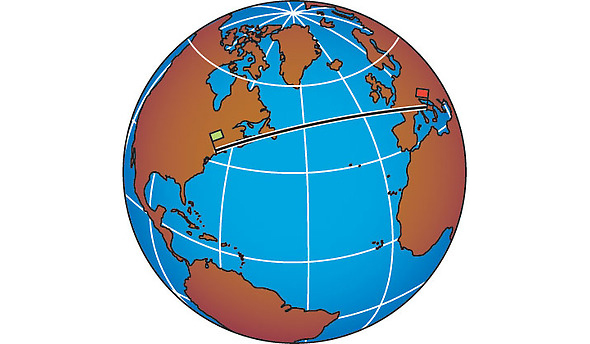
Такий шлях на кулі називається дугою «великого кола». Як і прямі лінії в звичайному просторі, великі кола на сфері містять найкоротші шляхи між двома точками. Їх називають «великими», тому що вони є найбільшими колами, які ви можете отримати на сфері. Яскравими прикладами є екватор, меридіональні кола, які проходять через північний і південний полюси.
Іншою характеристикою, яка є спільною для прямих ліній і великих кіл, є те, що вони є найпрямішими шляхами. Це може звучати дивно: всі шляхи на кулі є кривими, тож що ми маємо на увазі, кажучи «найпряміші»? Що ж, деякі шляхи є кривіші за інші. Великі кола не створюють жодної додаткової кривизни, понад ту, яку вони змушені створювати, тримаючись поверхні сфери.
Ось як це можна унаочнити. Уявіть, що ви їдете на дуже маленькому ровері поверхнею кулі і намагаєтеся триматися певного шляху. Якщо він є частиною великого кола, вам ніколи не треба буде повертати кермо. Саме у цьому сенсі великі кола є «прямими». І навпаки, якщо ви намагаєтеся їхати вздовж паралелі поблизу одного з полюсів, вам постійно треба буде повертати кермо.
Звісно, порівняно з іншими поверхнями, площина і сфера є надміру простими. Поверхня людського тіла, консервної бляшанки чи бублика була б типовішою: усі вони мають набагато менше симетрії, а також різні типи заглибин і прохідних отворів, що робить набагато складнішою навіґацію ними. У цьому загальнішому формулюванні задачі знаходження найкоротшого шляху між двома точками стає набагато складнішим. Тож замість того, щоб заглиблюватися в технічні подробиці, зосередьмося на інтуїтивному підході. Саме тут нам згодяться ґумові стрічки.
Отож уявіть гладку еластичну стрічку-тасьму, яка завжди стягується на скільки може, прилягаючи до поверхні. З її допомогою ми легко можемо визначити найкоротший шлях між Нью-Йорком і Римом чи, коли вже про це зайшла мова, між двома точками на будь-якій поверхні. Прив'яжіть кінці тасьми до точок відправлення і прибуття й дозвольте їй туго натягнутися, прилипаючи до поверхні. Коли тасьма є настільки тугою, наскільки дозволяють ці обмеження, готово! Вона прокреслює найкоротший шлях.
На трохи складнішій поверхні, ніж площини і сфери, може виявитись щось дивне і нове: може існувати багато локально найкоротших шляхів між тими самими двома точками. Наприклад, розгляньмо поверхню бляшаної пушки, де одна точка лежить прямо під іншою.
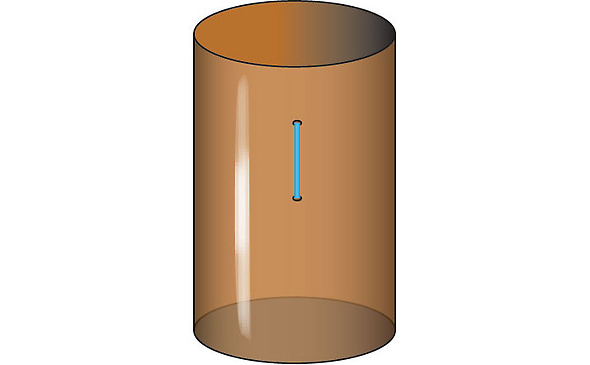
Тоді найкоротшим шляхом між ними є, очевидно, відрізок прямої, як показано вгорі, і наша еластична тасьма знайде це рішення. То що тут нового? Циліндрична форма бляшанки відкриває нові можливості для всіх типів вигинів. Припустімо, нам треба, щоб тасьма оповила циліндр, перед тим як з'єднається з другою точкою. Тож тепер тасьма натягується туго, утворюючи спіраль, як на давніх вивісках цирульників.
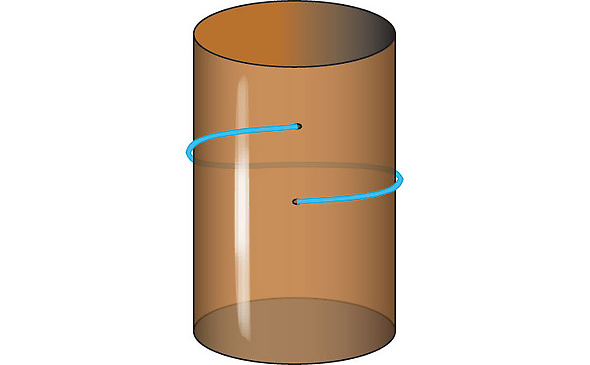
Цей ґвинтовий шлях є ще одним розв'язком проблеми найкоротшого шляху, у тому сенсі, що це найкоротший з усіх можливих близьких шляхів. Якщо ви трохи зсунете тасьму, вона обов'язково стане довшою, а потім знову стягнеться до ґвинтової лінії. Ви можете сказати, що це «локально» найкоротший шлях — місцевий чемпіон серед усіх тих, які один раз обмотуються довкола циліндра. (До речі, саме тому дисципліну називають «диференціальною» («різницевою») геометрією; вона вивчає вплив малих локальних відмінностей на різні типи форм, як-от різниця у довжині між ґвинтовою лінією та її сусідами).
Однак це не все. Є ще один чемпіон, який намотується двічі, і ще один, який оповивається тричі, і т.д. Є нескінченно багато локально найкоротших шляхів на циліндрі. Звісно, жодна з цих ґвинтових ліній не є «ґлобально» найкоротшим шляхом. Шлях по прямій є коротшим, ніж усі вони.
Аналогічно поверхні з дірами і ручками допускають багато локально найкоротших шляхів, які відрізняються своїми способами обвивання довкола різних частин поверхні. Відео, зроблене колись математиком Конрадом Польтіром з Берлінського вільного університету, ілюструє неєдиність цих локально найкоротших шляхів — чи «геодезичних ліній» — на поверхні уявної планети, яка має форму вісімки, поверхні, яку в професійних колах називають «подвійним тором».
Червоні, жовті й зелені геодезичні лінії проходять різними частинами планети, у такий спосіб утворюючи петлі. Але спільною для них усіх є більша прямота порівняно з поблизькими шляхами. Й аналогічно, як прямі на площині чи великі кола на сфері, ці геодезичні лінії є найпрямішими, наскільки це можливо, кривими на поверхні. Вони вигинаються, щоби пристосуватися до поверхні, але не звиваються по ній. На іншому його відео мотоцикл їде вздовж геодезичної автостради на подвійному торі, дотримуючись рельєфу місцевості. Цікавим є те, що мотоциклетне кермо заблоковане. Ним не треба кермувати, щоб залишатися на дорозі. Це акцентує попередні інтуїтивні уявлення, що геодезичні лінії, як і великі кола, є природним узагальненням прямих ліній.
З усіма цими польотами фантазії у вас може виникнути питання, чи геодезичні лінії мають щось спільне з реальністю. Ясна річ, мають. Ейнштейн показав, що світлові промені тримаються геодезичних ліній, ширяючи всесвітом. Славнозвісний залом світла зірок поблизу сонця, який виявили під час сонячних затемнень 1919 р., підтвердив, що світло поширюється по геодезичних лініях через викривлений простір-час, викривляючись через ґравітацію сонця.
На більш приземленому рівні математика знаходження найкоротших шляхів є вкрай необхідною у всьому: від навіґаційних систем GPS в наших автівках до маршрутизації інформаційного потоку в Інтернеті. Втім у цих ситуаціях відповідним простором є велетенський лабіринт адрес і веб-посилань, на відміну від гладких поверхонь, які ми розглядали вище, і математичні проблеми пов'язані зі швидкістю алгоритмів — яким є найефективніший спосіб знайти найкоротший шлях через мережу? Беручи до уваги міріади потенційних шляхів, завдання могло б виявитися непідйомним, якби не проникливість математиків і програмістів, які здолали його.
Подекуди, коли люди кажуть, що найкоротшою відстанню між двома точками є пряма лінія, вони говорять це в переносному значенні, з відтінком насмішки і обстоюючи здоровий глузд. Іншими словами, чим простіше, тим краще. Та подолання перешкод може посприяти зародженню великої краси — тим більше, що в мистецтві, і в математиці, часто більш плідним є накладати обмеження на самих себе. Згадаймо хайку, або сонети, чи розповідь про ваше життя в шести словах. Те саме стосується і до всієї математики, яка була створена, щоб знайти найкоротшу відстань між двома точками, коли не можна обрати легкий шлях.
Дві точки. Багато шляхів. Математичне блаженство.
Steven Strogatz
The Joy of X
Зреферувала Галина Грабовська
30.09.2016
