Групи каменів

Про математику. Від основ до незбагненного.

Як і все інше, арифметика має свою серйозний і грайливий бік.

Серйозний бік — це те, що ми всі вчили в школі: як працювати з колонками цифр, додаючи їх, віднімаючи їх, перемолочуючи їх табличними розрахунками, необхідними для податкових декларацій і річних звітів. Цей бік арифметики є важливим, практичним і — для багатьох людей — невтішним.

Грайливий бік арифметики нам менш знайомий, хіба що ви вивчали вищу математику. Втім, по своїй суті в цьому немає нічого вищого. Це настільки ж природно, як і цікавіть дитини.

У своїй книзі "Ламентація математика" Пол Локхарт виступає за такий освітній підхід, в якому числа розглядаються більш конкретно, ніж зазвичай: він просить нас уявити собі їх в якості груп каменів. Наприклад, шість відповідає такій групі каменів, як ця:

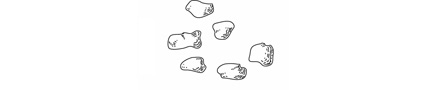
Скоріше за все, ви не бачите тут нічого особливого і це вірно – якщо ми не поставимо додаткових вимоги до чисел, всі вони виглядають більш-менш однаково. Наш шанс бути креативним полягає в тому, що ми питаємо в них.

Наприклад, давайте зосередимося на групах, що мають від 1 до 10 каменів, і запитаємось, які з них можуть бути перескладені так, щоб вийшов квадрат. Можуть тільки дві з них: 4 і 9. І це тому, що 4 = 2 × 2 і 9 = 3 × 3; ми отримуємо ці числа "підносячи до квадрату" якесь інше число (фактично, роблячи квадратну форму).

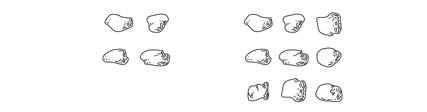
Трошки легше визначити групи каменів, які можуть бути акуратно складені в прямокутники з двома рядами, які виступають парно. Це можливо якщо є 2, 4, 6, 8, або 10 каменів; число повинно бути парним. Всі інші числа від 1 до 10 "непарні" — завжди залишають якийсь непарний камінь, що трохи стирчить.

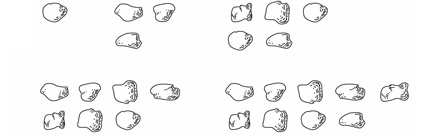
Проте, не все втрачено для цих кострубатих чисел. Якщо ми двоє з них додамо докупи, їхні виступи-протуберанці співпадуть, і в сумі отримаємо парно; Непарне +  Непарне = Парне.

Втім, коли справа доходить до прямокутників, деякі числами, такі як 2, 3, 5 і 7, є по справжньому безнадійними. Вони не можуть сформувати жоден вид прямокутника крім простої лінія з каменів. Ці дивно негнучкі числа є знаменитими "простими" числа.

Отже, ми бачимо, що числа мають особливості структури, які наділяють їх характерними рисами. Але, щоб побачити всю палітру їхньої поведінки, нам треба вийти за межі окремих чисел і подивитися, що відбувається, коли вони взаємодіють.

Наприклад, замість того, щоб додавати тільки два непарні числа, припустимо, що ми послідовно додаємо всі непарні числа, починаючи з 1:

1 + 3 = 4
1 + 3 + 5 = 9
1 + 3 + 5 + 7 = 16
1 + 3 + 5 + 7 + 9 = 25

Вражаюче: виявляється, що всі ці суми завжди є ідеальними квадратами. (4 і 9 ми бачили у формі розглянутих раніше квадратів, а 16 = 4 × 4 і 25 = 5 × 5.) Швидка перевірка показує, що це правило продовжує діяти для все більших і більших непарних чисел; це, очевидно, буде вірно аж до безкінечності. Але, який може бути зв'язок між непарними числами, з їх незграбних придатками і класичними симетричними числами, які формують квадрати? Правильно розклавши наші камені, ми зможемо змусити цей несподіваний зв'язок виглядати очевидним – що є критерієм елегантного доказу.

Головне, це усвідомити, що непарні числа можуть утворювати L-подібні форми, відсуваючи свої протуберанці в кут. І коли ви послідовні складете докупи L-форми, ви отримаєте квадрат!

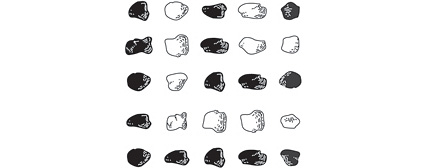
Цей стиль мислення з'являється в іншій книжці, хоча і з цілком інших літературних причин. В чарівному романі Йоко Огава "Домогосподарка і професор" показано кмітливу, але неосвічену молоду жінку з 10-річним сином, котру найняли для догляду за професором, літнім математиком, який отримав черепно-мозкову травму, яка залишає його всього 80 хвилин короткочасної пам'яті. Не орієнтуючись в теперішньому, і один у своєму ветхому котеджі, не пам’ятаючи нічого крім своїх цифр, професор намагається спілкуватись з домогосподаркою єдиним відомим йому способом: запитуючи про розмір її взуття або день її народження і зав’язує невимушену математичну розмову на тему статистики її даних. Професор виявляє особливу симпатію також і до сина домогосподарки, якого він називає Корінь, тому що плоска вершина голови хлопчика нагадує йому математичний символ квадратного кореню √

Одного дня професор дає Кореню маленьке завдання: чи може він знайти суму всіх чисел від 1 до 10? Після того, як Корінь уважно додав числа і повернувся з відповіддю (55), професор просить його знайти кращий спосіб. Чи може він знайти відповідь без додавання чисел? Корінь штовхає крісло і кричить: "Це нечесно!"

Але мало-помалу Домогосподарка втягується в світ чисел і таємно сама починає досліджувати загадку. "Я не знаю, чому мене так втягнула дитяча математична проблема без жодної практичної цінності," — каже вона. "Спочатку я була свідома того, що хочу догодити професору, але поступово це почуття відійшло і це стало битвою між проблемою і мною. Зранку, коли я прокинулась, рівняння чекало на мене:

1 + 2 + 3 + … + 9 + 10 = 55

і воно слідувало за мною протягом усього дня, так ніби було витавруване на моїй сітківці і його не можна було ігнорувати ".

Є декілька способів вирішення проблеми Професора (побачимо, скільки ви зможете знайти). Сам професор аргументує так, як ми зробили це вище. Він інтерпретує суму від 1 до 10 у вигляді трикутника каменів, з 1 каменем в першому ряді, 2 у другому і так далі, до 10 каменів в 10-му ряді:

Сам вигляд цієї картини дає чітке розуміння негативного простору. Він видається тільки наполовину завершеним. І це спонукає до творчого стрибка. Якщо ви скопіюєте трикутник, перевернувши його догори ногами і додасте, припасуєте його, як половину, що бракує до тої половини, що вже є, ви отримаєте щось набагато простіше: прямокутник з 10 рядами в кожному 11 каменів, в сумі 110.

Так як початковий трикутник це половина цього прямокутника, необхідна нам сума має складати половину 110, або 55.

Погляд на числа як групи каменів може здатися незвичним, але, насправді, цей метод настільки ж давній, як і сама математика. Цю спадщину відображає слово “calculus” ("калькулювати, рахувати") - воно походить від латинського слова calculus, що означає камінець, який використовували для рахування. Для того, щоб отримувати задоволення від праці з числами ви не повинні бути Айнстайном (що німецькою означає "один камінь"), але це може допомогти вам тримати камені у вашій голові.

Steven Strogatz
The Joy of X
Зреферував Михайло Мишкало