Мислити групами

Про математику. Від основ до незбагненного.

Виробники матраців рекомендують періодично перевертати матраци, можливо, пам'ятаючи про таких, як я. Але яка система найкраща? Як саме ви мали б повернути матрац, щоб у підсумку дістати найрівномірніше його зношення?

Браян Гейс досліджує цю проблему в титульному есеї своєї книжки «Теорія груп у спальні» (Group Theory in the Bedroom). Без двозначних сенсів: «група», про яку тут йдеться, — це сукупність математичних дій, тобто усі можливі способи того, як ви можете перекинути, повернути чи перевернути матрац, щоб він усе ще акуратно лежав на рамі ліжка.

Вивчаючи матрацну математику, я сподіваюся дати вам загальніше відчуття теорії груп, одного з найуніверсальніших розділів математики. Вона лежить в основі всього: від хореографії контрдансу та фундаментальних законів фізики елементарних частинок до мозаїк Альгамбри і їхніх хаотичних двійників, як на цьому зображенні.

Як свідчать ці приклади, теорія груп перекидає мости між наукою і мистецтвом. Вона звертається до того, що є спільним для двох культур, — до постійного захоплення симетрією. Однак оскільки теорія груп містить такий широкий ряд феноменів, то обов'язково є абстрактною. Вона зводить симетрію до її суті.

Зазвичай ми думаємо про симетрію як про властивість форми. Але теорії груп зосереджуються більше на тому, що ви можете зробити з формою — і насамперед на всіх способах, за допомогою яких ви можете змінити її, при тім залишаючи незмінним щось, що властиве їй. Якщо точніше, вони шукають усі трансформації, які залишають форму незмінною, взявши до уваги певні обмеження. Ці трансформації називають «симетріями» форми. Разом вони формують «групу», сукупність трансформацій, зв'язки між якими визначають найбільш базову архітектуру форми.

Якщо йдеться про матрац, то трансформації змінюють його положення в просторі (це те, що змінюється), водночас підтримують його ригідність (це обмеження). І після того, як розвіється дим, матрац має акуратно лягти в прямокутну раму ліжка (це те, що залишається незмінним). Враховуючи ці правила в натурі, подивімося, які перетворення мають право членства в цій маленькій ексклюзивній групі. Виявляється, тільки чотири з них.

Перша трансформація — «нічого-не-робити», лінивий, але популярний вибір, який залишає матраци недоторканими. Вона, звичайно, відповідає всім правилам, але не надто помагає продовжити життя вашого матраца. Проте дуже важливо долучити її до групи. Для теорії груп вона відіграє ту саму роль, що й нуль для додавання чисел або одиниця для множення. Математики називають її «одиничним елементом» (identity element), отже, я позначатиму її символом I.

Наступними будуть три справжні способи перекидання матраца. Щоб розрізняти їх, корисно буде позначити цифрами кути матраца:

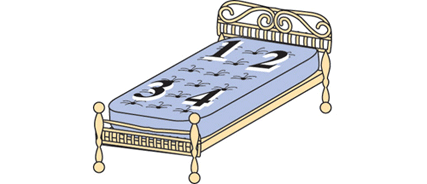
Перший спосіб перекидання зображено на початку цього тексту. Симпатичний джентльмен у смугастій піжамі намагається перекинути матрац, повертаючи його на 180 градусів навколо довгої осі рухом, який я назву H — «горизонтальне перекидання» (horizontal flip).

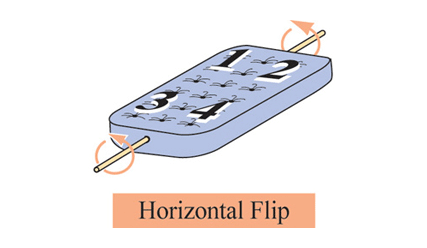
Більш сміливий і нерозважний спосіб перекинути матрац — це «вертикальний поворот» (vertical flip) V. Цей маневр міняє місцями голову і ноги матраца. Ви маєте поставити матрац вертикально, довгим кінцем так, що він майже сягне стелі, а тоді штовхнути його кінець через голову. Чистий ефект, крім дуже глухого удару, полягає в тому, щоб повернути матрац на 180 градусів навколо осі, як це показано внизу.

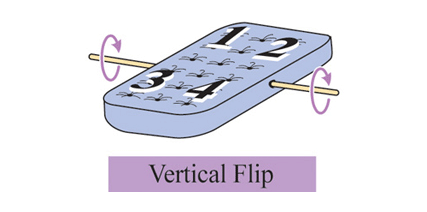
Остання можливість — це крутнути матрац на 180 градусів, не піднімаючи його з ліжка.

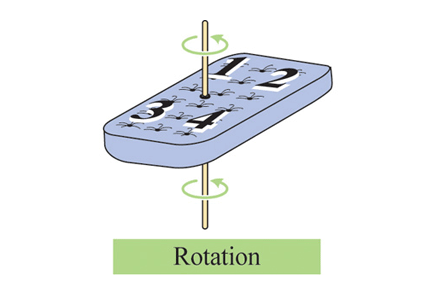
На відміну від поворотів H і V, це «обертання» (rotation) R залишає нагорі верхню поверхню. Це стане очевидно, якщо ми поглянемо на матрац згори — тепер уявіть, що він є прозорим, і простежте за числами в куті кожної з можливих трансформацій.

Горизонтальне перевертання повертає числа у їх дзеркальні відображення. Воно також переставляє їх так, що 1 і 2 міняються місцями, як 3 і 4.

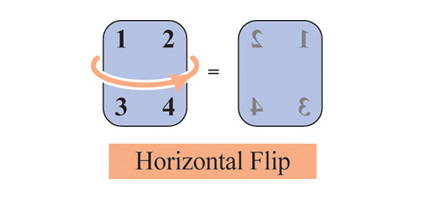
Вертикальне перевертання переставляє числа інакше і, окрім їх віддзеркалювання, ставить їх з ніг на голову.

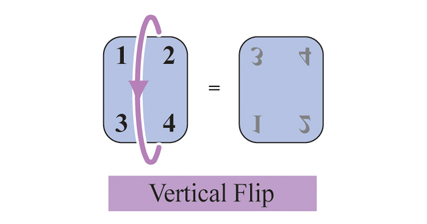
Зате обертання не ґенерує жодних дзеркальних відображень. Воно просто повертає числа догори ногами, цього разу змінюючи 1 на 4 і 2 на 3.

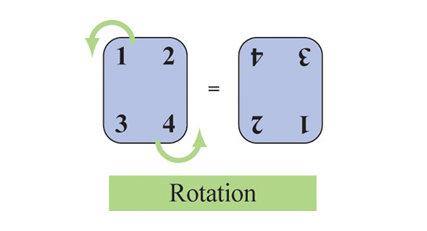
Проте суть не в цих деталях. Важливо те, як трансформації пов'язані одна з одною. Зразки їх взаємодії кодують симетрію матраца.

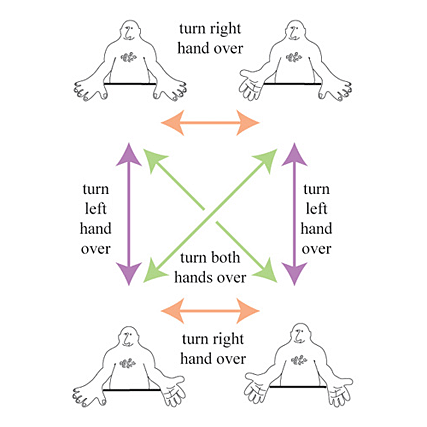
Наступна схема поможе нам показати ці зразки з мінімальним витрачанням зусиль. (У чудовій книжці «Візуальна теорія груп» (Visual Group Theory) Натана Картера рясніє такими зображеннями. Це один з найкращих вступів до теорії груп або до будь-якого розділу вищої математики, що я читав).

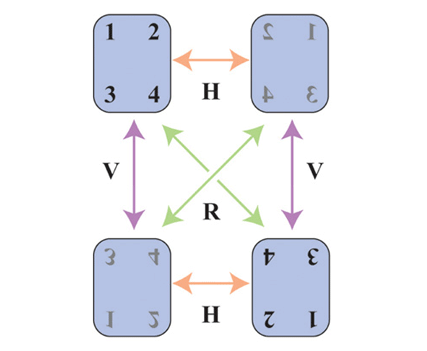
У кутах схеми показано чотири можливі «стани» матраца. Верхній ліворуч є стартовим пунктом. Кольорові стрілки показують рух матраца з одного стану в інший.

Наприклад, зелена стрілка, яка показує рух з верхнього лівого до нижнього правого кута, відображає дію обертання R. Та сама зелена лінія також має стрілку з іншого боку, бо якщо ви двічі зробите R, це те саме, що й нічого не робити.

Це б не мало дивувати. Це просто означає, що перекинути матрац з ніг на голову, а потім ще раз — те саме, що повернути матрац до його початкового стану. Ми можемо належно підсумувати це рівнянням RR = I, де RR означає двічі робити R, а I — це «нічого-не-робити», одиничний елемент. У цьому сенсі горизонтальне і вертикальне перевертання-трансформації також анулюють самі себе: HH = I і VV = I.

Схема втілює багатство іншої інформації. Вона, наприклад, показує, що з ризиком для життя вертикальний поворот V еквівалентний HR, горизонтальному повороту з наступним обертанням — набагато безпечніший шлях для досягнення такого самого результату. Щоб перевірити це, почніть зі стартового стану у верхньому лівому куті. Голова матраца прямує на схід вздовж H до наступного стану, а звідти діагонально рухається на південний захід вздовж R. Оскільки ви доходите до того самого стану, який отримали б, якби просто виконали V, діаграма демонструє, що HR = V.

Зауважте також, що порядок виконання цих дій не має значення: HR = RH, оскільки обидва способи приводять до V. Ця індиферентність до порядку актуальна для будь-якої пари дій. Ви маєте думати про це як про узагальнення комутативного закону додавання простих чисел, x і y, згідно з яким x + y = y + x. Але будьте уважні: матрацна група є особливою. Багато інших груп порушують комутативний «закон». Ті, кому пощастило дотримуватися його, є особливо чистими і простими.

І тепер до результату. Схема показує, як отримати спосіб найрівномірнішого зношення матраца. Працюватиме будь-яка стратегія, яка періодично застосовує всі чотири стани. Наприклад, чергування R і H зручне, оскільки воно, оминаючи V, не вимагає великих зусиль. Щоб допомогти вам запам'ятати це, деякі виробники пропонують мнемоніку «навесні крутити і восени перевертати » (spin in the spring, flip in the fall).

Матрацна група спливає в деяких несподіваних місцях — від симетрії молекул води до логіки пари електричних перемикачів. Це одна з чарівних рис теорії груп. Вона показує єдність речей, які в іншому разі здавалися б зовсім непов'язаними між собою… наче в тому анекдоті про те, як фізик Річард Фейнман дістав відтермінування призову в армію.

Військовий психіатр попросив Фейнмана виставити руки так, щоб він міг оглянути їх. Фейнман витягнув їх, одна долоня вгору, інша вниз. «Ні, не так», — сказав психіатр. Тож Фейнман повернув обидві руки, залишивши одну долоню донизу, іншу догори.

Фейнман не просто бавився в маніпулятивні техніки; він насолоджувався гумором теорії груп. Якщо ми розглянемо всі можливі способи того, як він міг виставити свої руки, плюс розмаїті переходи між ними, стрілки сформують той самий зразок, що й у матрацній групі!

Але якщо все це робить справу з матрацами надто складною, то, можливо, реальна з того наука — яку ви вже знали — коли  вас щось тривожить, просто переспіть з тим.

Steven Strogatz
The Joy of X
Зреферував Михайло Мишкало