Те, що прості числа та степені двійки зачаровують багатьох людей, не дивує. Виявилося, що всі числа розділилися на два табори: цікаві та нудні. Чому?
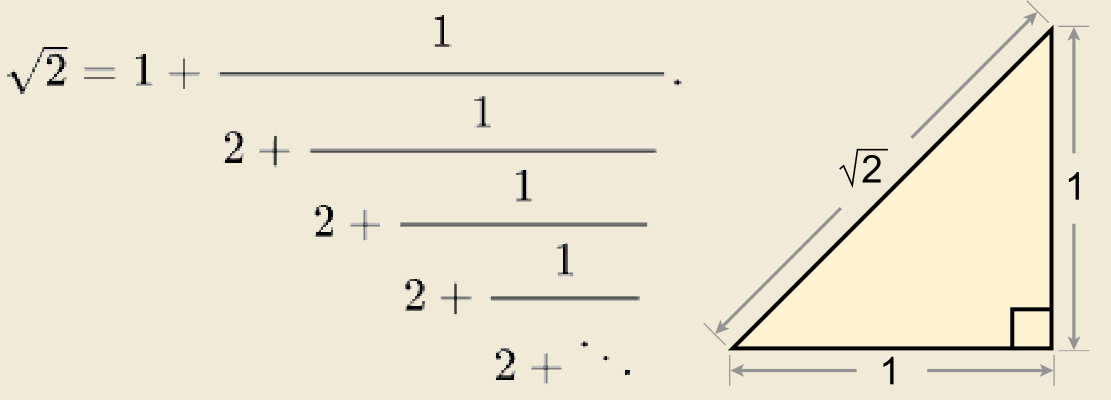
Яке ваше улюблене число? Багато людей, мабуть, назвуть ірраціональні числа – такі як пі (π), число Ейлера (e) або квадратний корінь з 2. Але навіть серед натуральних чисел можна знайти значення, які зустрічаються в найрізноманітніших контекстах: сім гномів, сім смертних гріхів, 13 як нещасливе число – і 42, яке популяризував роман «Путівник по Галактиці» Дугласа Адамса.
А як щодо більшого значення, такого як 1729? Для більшості людей це число, напевно, не здається особливо захопливим. На перший погляд, воно видається відверто нудним. Зрештою, воно не є ні простим числом, ні степенем 2, ні квадратом якогось цілого числа. Та й цифри в ньому не підпорядковуються жодній очевидній закономірності. Так само думав математик Ґодфрі Гарольд Гарді (1877–1947), коли сідав у таксі з ідентифікаційним номером 1729. Він власне відвідував у лікарні свого хворого колегу Срініваса Рамануджана (1887–1920) і розповів йому про "нудний" номер таксі. Гарді сподівався, що це не є поганою прикметою. Рамануджан одразу ж заперечив своєму другові: "Це дуже цікаве число; це найменше число, яке можна виразити як суму двох кубів двома різними способами".
Тепер ви можете задатися питанням, чи може взагалі існувати число, яке не було б цікавим. Це питання швидко веде до парадоксу: якщо дійсно існує значення n, яке не має жодних цікавих властивостей, то саме цей факт робить його особливим. Але все-таки існує спосіб досить об'єктивно визначити цікаві властивості числа – і, на превеликий подив математиків, дослідження 2009 року показало, що натуральні числа (цілі невід’ємні числа) діляться на два чітко окреслені табори: цікаві та нудні.
Вичерпна енциклопедія числових послідовностей дає можливість дослідити ці дві протилежні категорії. Ідея створення такого збірника виникла у математика Ніла Слоуна в 1963 році, коли він писав докторську дисертацію. У той час йому довелося обчислити висоту значень у типі графу, який називається деревоподібною топологією, і натрапив на послідовність чисел: 0, 1, 8, 78, 944,... Він ще не знав, як точно обчислити числа в цій послідовності, і хотів дізнатися, чи його колеги вже стикалися з подібною послідовністю під час своїх досліджень. Але на відміну від логарифмів чи формул, не існувало жодного реєстру для послідовностей чисел. Отже, через десять років Слоун опублікував свою першу енциклопедію "Довідник цілочислових послідовностей", що містила близько 2400 послідовностей, які також виявилися корисними при виконанні певних обчислень. Книга зустріла гаряче схвалення: "Є Старий Заповіт, Новий Заповіт і Довідник цілочислових послідовностей", – написав, за словами Слоуна, один захоплений читач.
Протягом наступних років до Слоуна надходили численні пропозиції більшої кількості послідовностей, а також з’явилися наукові статті з новими послідовностями чисел. У 1995 році це спонукало цього математика разом з його колегою Саймоном Плуффом опублікувати "Енциклопедію цілочислових послідовностей", що містила близько 5500 позицій. Контент продовжував невпинно зростати, але інтернет дозволив контролювати потік даних: у 1996 році з'явилася Інтерактивна енциклопедія цілочислових послідовностей (OEIS) у форматі без жодних обмежень їхню кількість, які можна записати. Станом на березень 2023 року вона налічує трохи більше 360 000 записів. Подати заявку може будь-хто, треба лише, вносячи послідовність, пояснити, як вона була згенерована і чому вона цікава, а також навести приклади, що пояснюють перші кілька членів. Після цього рецензенти перевіряють заявку і публікують її, якщо вона відповідає цим критеріям.

Послідовність "лінивого кельнера". Максимальна кількість частин p, яка може вийти з n розрізів.
Окрім загальновідомих послідовностей, таких як прості числа (2, 3, 5, 7, 11, ...), степені 2 (2, 4, 8, 16, 32, ...) або послідовність Фібоначчі (1, 1, 2, 3, 5, 8, 13, ...), каталог OEIS також містить екзотичні приклади, як-от кількість способів побудови стійкої вежі з n кубиків Lego розміром два на чотири, (1 , 24, 1560, 119580, 10166403,…) або «послідовність лінивого кельнера» (1, 2, 4, 7, 11, 16, 22, 29…), максимальна кількість шматочків торта, яку можна досягти за n розрізами.
Оскільки близько 130 осіб переглядають надіслані числові послідовності, а список із цими очевидними кандидатами існує вже кілька десятиліть і досить добре відомий серед математиків, збірник призначений для об’єктивного відбору всіх послідовностей. Це робить каталог OEIS придатним для вивчення популярності чисел. Відповідно, що частіше число трапляється у списку, тим воно цікавіше.
Так, принаймні, вважає Філіп Гульєльметті, який веде франкомовний блог Dr. Goulu. В одному з дописів Гульєльметті згадав твердження колишнього вчителя математики про те, що 1548 – довільне число без особливих властивостей. Насправді це число трапляється 326 разів у каталозі OEIS. Наприклад, воно зустрічається як "евентуальний період однієї клітини в клітинному автоматі за правилом 110 у циклічному всесвіті шириною n". Гарді також помилявся, коли назвав номер таксі 1729 нудним: 1729 з'являється 918 разів у базі даних (а також – часто – в телесеріалі "Футурама").
Відтак Гульєльметті взявся шукати справді нудні номери: ті, які майже не зустрічаються в каталозі OEIS, якщо взагалі там є. Останнє стосується, наприклад, числа 20067. Станом на березень це найменше число, яке не зустрічається в жодній із багатьох збережених послідовностей чисел. (Це лише тому, що в базі даних зберігаються перші 180 або близько того символів числової послідовності – інакше би у списку позитивних цілих чисел в ОЕІС з'явилося б кожне число). Тому значення 20067 здається досить нудним. Натомість для числа 20068, яке йде після нього, є шість записів.
Але універсального закону нудних чисел не існує, і статус 20067 може змінитися. Можливо, під час написання цієї статті було виявлено нову послідовність, в якій 20067 з'являється серед перших 180 символів. Однак записи в OEIS для певного числа підходять як показник того, наскільки воно є цікавим.
Далі Гульєльметті послідовно виводив кількість усіх записів для натуральних чисел і побудував графік результату. Він виявив хмару точок у формі широкої кривої, яка нахилена в бік великих значень. Це не дивно, оскільки лише перші члени послідовності зберігаються в каталозі OEIS. Однак дивно те, що крива складається з двох смуг, які розділені чітко видимим проміжком. Таким чином, натуральне число з'являється в базі даних OEIS або дуже часто, або вкрай рідко.

Розрив Слоуна. Якщо проаналізувати частоту натуральних чисел у каталозі OEIS, то можна виділити два типи: цікаві значення, тобто які з'являються часто (верхня смуга), і нудні числа (нижня смуга).
Захоплений цим результатом, Гульєльметті звернувся до математика Жана-Поля Делає, який регулярно пише науково-популярні статті для Pour la Science, франкомовного дочірнього видання Scientific American. Він хотів дізнатись, чи експерти вже досліджували це явище. Виявилося, що цього таки ніхто не досліджував, і Делає взявся за цю тему разом зі своїми колегами Ніколя Говрі та Гектором Зенілом і дослідив її ретельніше. Вони використали результати алгоритмічної теорії інформації, яка вимірює складність виразу довжиною найкоротшого алгоритму, який описує вираз. Наприклад, довільне п'ятизначне число, таке як 47934, описати складніше ("послідовність цифр 4, 7, 9, 3, 4"), ніж число 16384 (214). Згідно з теоремою з теорії інформації, числа з багатьма властивостями зазвичай також мають низьку складність. Тобто значення, які часто з’являються в каталозі OEIS, найімовірніше, будуть простими для опису. Делає, Говрі і Зеніл змогли показати, що теорія інформації передбачає подібну траєкторію для складності натуральних чисел, що показана на кривій Гульєльметті. Але це не пояснює видимий розрив у цій кривій, відомий як "розрив Слоуна", на честь Ніла Слоуна.
Троє математиків припустили, що розрив виникає через соціальні фактори, такі як перевага певних чисел. Щоб обґрунтувати це, вони провели так зване моделювання Монте-Карло: розробили функцію, яка дозволяє зіставити натуральні числа з натуральними – і робить це таким чином, що менші числа виводяться частіше, ніж більші. Дослідники ввели у функцію випадкові значення і побудували графік результатів відповідно до їхньої частоти. Це створило нечітку похилу криву, подібну до даних у каталозі OEIS. Але так само, як і при аналізі з теорії інформації, немає жодних слідів розриву.
Щоби краще зрозуміти, як виникає розрив, потрібно подивитися, які числа потрапляють до того чи іншого діапазону. Для невеликих значень, приблизно до 300, розрив Слоуна не дуже виражений. Лише для більших чисел розрив суттєво збільшується: близько 18 відсотків усіх чисел від 300 до 10 000 знаходяться в "цікавому" діапазоні, тоді як решта 82 відсотки належать до "нудних" значень. Виявляється, цікавий діапазон включає близько 95,2% всіх квадратів і 99,7% простих чисел, а також 39% чисел з багатьма простими множниками. Ці три класи вже становлять майже 88 відсотків цікавого діапазону. Решта значень мають вражаючі властивості, такі як 1111 або формули 2n + 1 і 2n – 1 відповідно.
Згідно з теорією інформації, особливий інтерес викликають ті числа, які мають низьку складність, тобто їх легко виразити. Але якщо математики вважають певні значення більш цікавими, ніж інші такої самої складності, то це, як стверджують Делає, Говрі і Зеніл, може призвести до розриву Слоуна. Наприклад: 2n + 1 і 2n + 2 однаково складні з точки зору теорії інформації, але значення тільки першої формули є в "цікавому діапазоні". Це тому, що такі числа дозволяють вивчати прості числа – так вони з’являються в багатьох різних контекстах.
Отже, поділ на цікаві та нудні числа, схоже, випливає з наших суджень – наприклад, із того, що ми надаємо значення простим числам. Якщо ви хочете дати справді креативну відповідь на запитання, яке ваше улюблене число, то можете назвати таке число, як 20067, яке ще не внесене в енциклопедію Слоуна.
Manon Bischoff
Auf der Suche nach der langweiligsten Zahl der Welt
Spektrum.de, 10.02.2023
Переклад: Роман Друль
18.03.2023