Про математику. Від основ до незбагненного.

Якось я отримав електронного листа від читачки на ім'я Кім Форбс. Її шестирічний син Бен поставив їй математичне питання, на яке вона не змогла відповісти, тож вона сподівалася, що я зможу допомогти:
Нині його 100-й день у школі. Він був дуже схвильований і розповів мені все, що знає про число 100, навіть те, що 100 – це парне число. Він навіть сказав мені, що 101 – це непарне число, а 1 млн. – парне тощо. Потім він зробив паузу і запитав: «А нескінченність є парною чи непарною?».
Я пояснив, що нескінченність не є ані парною, ані непарною. Вона не є числом у звичному розумінні і не скоряється правилам арифметики. Якби вона задовольняла ці правила, ми б отримали всеможливі протиріччя. Наприклад, «якби нескінченність була непарною, нескінченність помножити на 2 була би парною. Але вони обидві є нескінченностями! Отож уся ідея парності і непарності не має сенсу для нескінченності».
Кім відповіла:
Дякую. Бен задоволений цією відповіддю, йому подобається ідея, що нескінченність є достатньо великою, аби бути і парною, і непарною.
Хоча дещо в цьому тлумаченні перекручене (нескінченність не є ані парною, ані непарною, а не тією і тією одночасно), Бенове тлумачення вказує на більшу правду. Нескінченність може бути дивовижною.
Деякі з її найдивніших аспектів вперше стали очевидними наприкінці 1880-х, коли Ґеорґ Кантор написав свою революційну працю про «теорію множин». Кантор зокрема цікавився нескінченними множинами чисел і точок, як-от множини «натуральних чисел» {1, 2, 3, 4,…} і множини точок прямої. Він означив строгий спосіб порівнювати нескінченні множини і був приголомшений, коли виявив, що деякі нескінченності є більшими, ніж інші.
Тоді теорія Кантора збудила не тільки опір, а також обурення. Анрі Пуанкаре, один з тогочасних провідних математиків, назвав її «заразою». Однак інший велетень епохи, Давид Гільберт, вважав її важливим внеском і згодом заявив: «Ніхто не вижене нас з раю, який створив Кантор».
Моя мета — дати вам певне уявлення про цей рай. Але замість роботи безпосередньо з множинами чисел або точок, я буду дотримуватись підходу, запропонованого самим Гільбертом. Він наочно передав своєрідність і дивовижність Канторової теорії, розповівши притчу про великий готель, тепер відомий як Гільбертів готель.
Всі номери у ньому постійно зайняті, проте завжди знайдеться вільний.
У Гільбертовому готелі не просто сотні номерів, у ньому їх нескінченна кількість. Коли прибуває новий гість, управитель переселяє мешканця номера 1 в номер 2, з номера 2 в номер 3 і т.д. Це дозволяє вивільнити номер 1 для новоприбулого, а також розмістити усіх решта (хоча переселення створює їм незручності).
Тепер припустімо, що прибула нескінченна кількість нових гостей, спітнілих і роздратованих. Нічого страшного. Менеджер не втрачає самовладання і переселяє пожильця з номера 1 в номер 2, з номера 2 в номер 4, з номера 3 в номер 6 і т. д. Цей трюк подвоєння робить доступними всі кімнати з непарними номерами — нескінченну їх кількість — для нових гостей.
Пізніше того самого вечора до готелю з гуркотом під'їздить колона автобусів, якій не видно кінця. Цих автобусів є нескінченна кількість, ба гірше: кожен з них напхом напханий нескінченною кількістю невдоволених людей, які вимагають, аби готель виправдав своє гасло — «В Гільбертовому готелі завжди є вільні номери».
Перед управителем вже поставала така проблема і він вирішує її одним махом.
Спочатку він робить трюк подвоєння. Перерозподілом наявних гостей по кімнатах з парними номерами вивільняє всі кімнати з непарними номерами, і це добрий початок, тому що тепер до свого розпорядження він має нескінченну кількість кімнат.
Та чи цього досить? Чи справді є стільки кімнат з непарними номерами, щоб розмістити велелюдну галасливу юрбу нових гостей? Це здається неможливим, оскільки щось на зразок «піднесеної до квадрату нескінченності» людей шумно вимагає цих кімнат. (Чому піднесена до квадрату нескінченність? Тому що ми маємо нескінченну кількість людей в кожному автобусі, яких також є нескінченна кількість, а це нескінченність помножена на нескінченність, хай що це означає).
І саме тут логіка нескінченності стає дуже химерною.
Зрозуміти, як управитель вирішить останню проблему, буде легше, коли ми уявимо собі усіх цих людей, яких він має розселити.
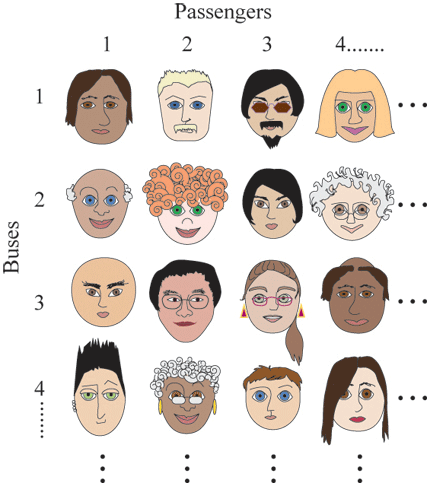
Звісно, ми не можемо показати тут всіх їх буквально, тому що рисунок мав би бути нескінченним в обох напрямах. Але скінченний варіант малюнка є достатнім. Суть в тому, що будь-який конкретний пасажир автобуса (скажімо, ваша тета Інес, яка приїхала у відпустку з Луїсвілля) точно з'явиться де-небудь на рисунку, якщо тільки ми додамо достатню кількість рядків і стовпчиків. У цьому сенсі кожен пасажир в кожному автобусі є врахований. Ви називаєте пасажира, і він або вона безсумнівно будуть зображені за певну скінченну кількість кроків на схід і на південь від кута малюнка.
Проблема управителя полягає в тому, щоб знайти спосіб пробратися через цей малюнок планомірно. Йому треба розробити схему виділення кімнат, аби кожен врешті-решт отримав свою, тільки-но скінченну кількість інших людей буде розселено.
На жаль, попередній управитель не розумів цього, через що і зчинився рейвах. Коли аналогічна колона з'явилася під час його чергування, він заходився розселяти всіх людей з автобуса 1 в такому сум'ятті, що до жодного іншого автобуса руки йому так і не дійшли, тож ці розлючені й крикливі пасажири були покинуті напризволяще. Зображена на малюнку нижче, ця недалекозора стратегія відповідає шляху, який йде на схід вздовж рядка 1 і не повертається назад.

Проте новий менеджер тримає все під контролем. Замість того, щоб прицювати лише з одним автобусом, він рухається по малюнку зиґзаґом, починаючи від кута, як показано нижче.

Він починає від пасажира 1 в автобусі 1 і дає йому першу вільну кімнату. Друга і третя вільні кімнати дістаються пасажирові 2 з автобуса 1 і пасажирові 1 з автобуса 2, обидва вони зображені на другій від кута малюнку діагоналі. Розселивши їх, менеджер береться за третю діагональ і видає ключі від кімнат пасажирові 1 з автобуса 3, пасажирові 2 з автобуса 2 і пасажирові 3 з автобуса 1.
Я сподіваюся, що метод менеджера — просування від однієї діагоналі до іншої — є зрозумілим з малюнку вгорі і що ви переконаєтеся, що до кожної окремої людини дійдуть через скінченну кількість кроків.
Тож, як і сказано в рекламі, у Гільбертовому готелі завжди є вільні номери.
Щойно наведене мною міркування є відомим в теорії нескінченних множин. Кантор використав його для доведення того, що додатних дробів (відношень p/q додатних цілих чисел p і q) є точно стільки само, скільки є натуральних чисел (1, 2, 3, 4, …). Це твердження є набагато сильнішим, ніж говорити, що обидві множини є нескінченними. Воно говорить, що вони є нескінченними точно такою самою мірою, у тому сенсі, що між ними може бути встановлена «взаємно однозначна відповідність».
Ви можете сприймати цю відповідність як набір пар, в якій кожне натуральне число утворює пару з додатним дробом і навпаки. Існування такого набору здається цілком несумісним зі здоровим глуздом: це той різновид софістики, який і спричинив неґативну реакцію Пуанкаре. Оскільки воно передбачає, що ми могли б зробити вичерпний перелік всіх додатних дробів, хоча вони навіть не мають найменшого елемента!
І тепер ми маємо такий перелік. Ми вже його знайшли. Дріб p/q відповідає пасажирові p в автобусі q і наведені вище міркування показують, що кожен з цих дробів може бути співвіднесений з певним натуральним числом 1, 2, 3,…, рівним номеру кімнати пасажира в Гільбертовому готелі.
«Ударом милосердя» стає Канторове доведення, що деякі нескінченні множини є більшими, ніж інші. А саме множина дійсних чисел між 0 і 1 є «незліченною»: її не можна взаємно однозначно співвіднести з натуральними числами. Для готельної індустрії це означає, що якщо всі ці дійсні числа з'являться при рецепції і подзвонять у дзвінок, для них усіх не вистачить кімнат навіть в Гільбертовому готелі.
Доведення від супротивного: припустимо, що кожному дійсному числу виділена власна кімната. Тоді реєстр мешканців, ідентифікованих їхніми десятковими розкладами і пронумерованих номерами кімнат, буде виглядати так:
Кімната 1: 0,6708112345…
Кімната 2: 0,1918676053…
Кімната 3: 0,4372854675…
Кімната 4: 0,2845635480…
Пам'ятаймо, що це має бути повний перелік. Припускається, що кожне дійсне число між 0 і 1 десь з'явиться, на певному скінченному місці реєстру.
Кантор показав, що в такому переліку пропущено велику кількість чисел; в цьому полягає суперечність. Наприклад, щоб побудувати число, яке ніде не з'явиться в наведеному вище переліку, йдіть вниз по діагоналі і будуйте нове число із виділених жирним шрифтом цифр:
Кімната 1: 0,6708112345…
Кімната 2: 0,1918676053…
Кімната 3: 0,4372854675…
Кімната 4: 0,2845635480…
Утворений в такий спосіб десятковий дріб є 0,6975…
Але це ще не все. Наступний крок: беремо цей десятковий дріб і змінюємо всі його цифри, замінивши кожну з них довільною іншою цифрою між 1 і 8. Наприклад, ми можемо змінити 6 на 3, 9 на 2, 7 на 5 і т.д.
Цей новий десятковий дріб 0,325… вбиває наповал. Він точно не є в кімнаті 1, оскільки його перша цифра відмінна від першої цифри числа, яке є там. Він також не є в кімнаті 2, оскільки його друга цифра не збігається. Загалом, цей дріб відрізняється від n-го числа на n-ій десятковій позиції. Отож він ніде не з'являється в переліку!
Висновок той, що в Гільбертовому готелі всі дійсні числа розміститися не можуть. Їх є попросту забагато, нескінченність понад нескінченність.
І з цим скромним міркуванням ми підходимо до кінця серії статей, яка почалася 14 тижнів тому сценою в іншому уявному готелі. Персонаж із передачі «Вулиця Сезам» (Sesame Street) на ім'я Гамфрі працює на роздачі при ляді в готелі «Пухнасті лапи» (The Furry Arms), де приймає замовлення із заповненої пінґвінами кімнати: «риба, риба, риба, риба, риба» — і незабаром дізнається про могутність чисел.
Ця мандрівка від риби до нескінченності була тривалою. Я сподіваюся, ви дістали від неї таку саму насолоду, як і я.
Steven Strogatz
The Joy of X
Зреферувала Галина Грабовська
28.10.2016
