
Тема сьогоднішньої доповіді – «Міста і закони». Напередодні у рамках лекційного циклу «Феномен життя» Владислав Соболевський з Університету Нью-Йорку виступив з темою «Міста як джерело Big Data». У лекції він розглянув проблему колосального масиву інформації, який породжує місто, коли ви, наприклад, розраховуєтеся кредитками чи використовуєте транспортні картки для проїзду. Для характеристики цього масиву недостатньо таких префіксів, як «мега», «гіга» чи «тера» – потрібні спеціальні слова. Він також говорив про те, скільки всього корисного можна зробити у місті на підставі цієї інформації. Я ж сьогодні говоритиму не настільки про застосування а передусім про підставові поняття. А саме мова йтиме про закони самоорганізації міста, які аналогічні до тих, які діють в будь-яких складних системах. Слово «закони» у назві лекції слід розуміти не як правила, встановлені людиною, а як статистичні закономірності, спільні для міст, що різняться за географічним розташуванням, рівнем економічного розвитку, історичною та культурною традицією. На відміну від законів, встановлених людиною, ці закони не можна обійти, а їх незнання не позбавляє неминучості їх виконання.
Підзаголовок лекції – «Міста як складні системи». Наука про складні системи – це дисципліна, яка на сьогодні вже серйозно заявила про своє виникнення і зрілість, хоча все ще активно розвивається. У цьому контексті я хочу розглянути міста з погляду колективної поведінки їх мешканців. Кожен із нас щоденно виконує якісь конкретні, індивідуальні дії: ходить на роботу, відвідує церкву, користується громадським транспортом. Але водночас всі ми є частинками колективного організму міста, який живе своїм життям. Побачити цей колективний вимір дуже складно, так само, як було би складно з перспективи клітини дивитися на організм в цілому. Але саме це і є ключовим у складних системах, які можна означити як сукупність елементів, колективна поведінка яких зовсім не очевидна з поведінки однієї складової частинки. Сьогодні мова піде про різні приклади такої поведінки: економічний, транспортний, комунікаційний, соціальний. Ітиме мова про універсальні закони, яким підлягають властивості притаманні місту як цілому, його організації, розвитку, кореляціям між різними процесами, що визначають міське життя. Аналіз і розуміння цих законів є одним із завдань науки про складні системи – нової дисципліни, що знаходиться на перетині фізики, біології, економіки, соціології і гуманітарних наук.
Вивчення складних систем – це нова галузь науки, яка досліджує те, як стосунки між частинами породжують колективну поведінку системи. Одна із статей, з якої починалась ця наука, називалась «More is different» («Більше означає інакше»). Ці слова належать Філіпу Андерсону, лауреату Нобелівської премії з фізики. І, значною мірою, моя доповідь (як і наука про складні системи в цілому) базуватиметься на концептуальному апараті фізики, зокрема тієї її ділянки, яка називається статистичною фізикою. Приклади складних систем можна знайти в дуже різних сферах життя природи чи життя суспільства. Їм притаманні кілька ключових ознак. По-перше, самоорганізація. Наочний приклад самоорганізації – політ зграї ворон. Кожна ворона, здається, веде себе так, як хоче, але коли ми подивимось на їх зграю у вечірньому небі, то здається, що це окреме, велике, розумне ціле, яке зберігає форму і знає, куди рухатись. По-друге, емерджентність. Цей термін походить від англійського слова «to emerge» (виникати) і означає виникнення в системи якоїсь нової якості, якої немає в її елементів поодинці, наприклад пізнання у мозку. По-третє, чутливість. Навіть найменші зміни в початкових параметрах системи можуть привести до кардинальних змін системи як цілого. Це зафіксовано в афоризмі про метелика, який своїми крильцями породжує ураган в Карибському морі. По-четверте, поведінка типу розподілу із «товстим хвостом», що, як правило, описується стененевим законом. Тут мова йде про те, що події, які, за звичайною гаусовою статистикою мали б відбуватися дуже рідко, насправді відбуваються набагато частіше. По-п'яте, адаптивна взаємодія. Ця властивість складних систем означає зміну взаємодії між агентами в залежності від поведінки всієї системи.
Згадавши загальні ознаки поведінки складних систем, тепер продемонструємо ці ознаки на прикладі міст. На поданих нижче схемах видно своєрідну дату-Рубікон. Це 2008 рік – рік, коли більшість людей на планеті почала жити в містах.
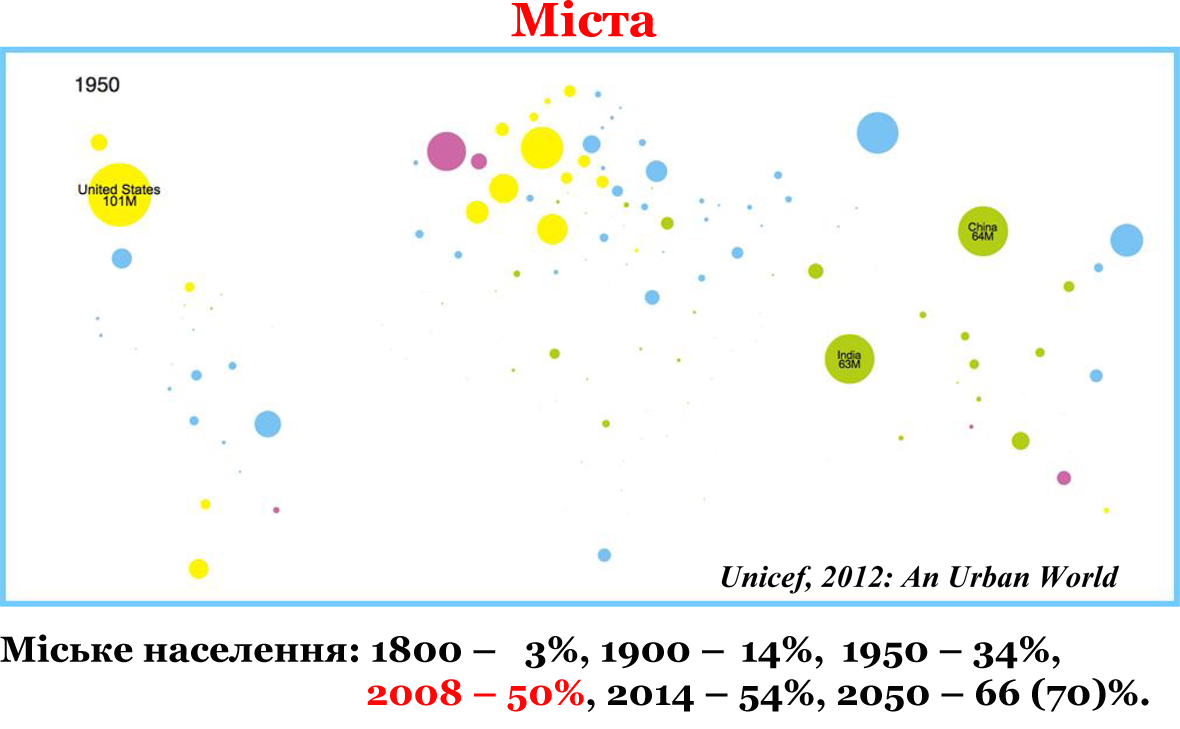
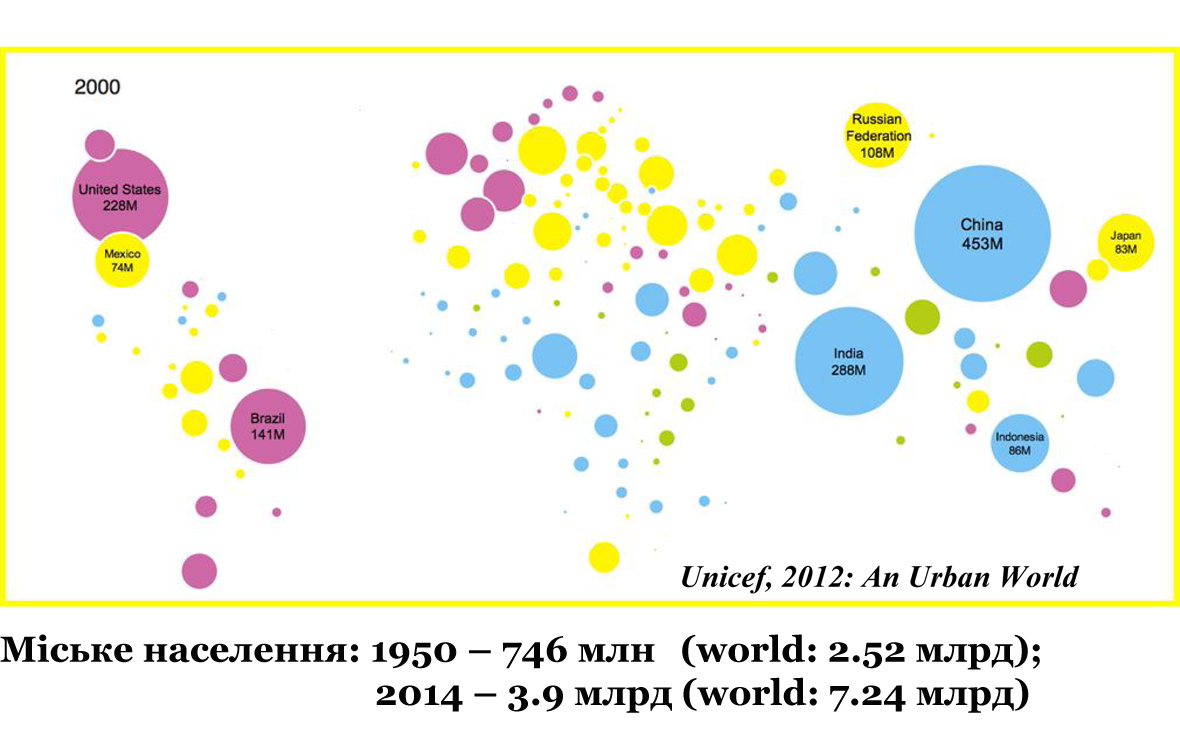

Зростання чисельності населення міст в окремих країнах (розмір кружечків) та відсоткове співвідношення населення у містах до загальної чисельності населення в реґіонах (подане у кольорі). Три рисунки відповідають даним за 1950 і 2000 рр. в порівнянні з прогнозом на 2050 р. Цит. за: Unicef, 2012: An Urban World
У 1800 р. лише 3% населення Землі жили в містах. У 1900 – 14%, у 2008 – 50%, а в 2014 – 54%. Згідно прогнозів, у 2050 р. ⅔ всіх усіх мешканців Землі житимуть в містах. На мапах подана кількість міського населення у різних країнах. У 1950 р., коли населення світу становило 2,5 млрд., в містах жили 677 млн. У 2014 р. в містах живе вже 4 млрд., тоді як населення світу становить 7 млрд. Слід зазначити також, що урбанізація, яка активно триває протягом останніх 200 років, сьогодні відбувається передусім в слаборозвинених країнах.
Міста – це складні системи, яким притаманна кожна із перелічених вище характерних рис. Особливості міста, як складної системи, можна виразити математично. Про різні кількісні характеристики такого опису я говоритиму далі. Для початку, продемонструємо як виникає степенева залежність, що характеризує вимірність міста, його комунікаційних, транспортних систем. Наприкінці ХХ ст. на міста почали дивитися з погляду такої особливості складних систем, як неціла вимірність. Що таке вимірність, ми пам'ятаємо зі школи. Те, що має лишень довжину, має є вимірність 1, довжину і ширину – 2, довжину, ширину і висоту – вимірність 3. Вимірність прямої становить 1, квадрату чи плоскої фігури – 2, вимірність кубу – 3. Скажімо, об'єм куба становить r³, а об'єм сфери складає ⁴/₃πr³. Коефіцієнт інший, але і для куба і для сфери це завжди r³, і цей «куб» показує, що об'єкти, про які йде мова, тривимірні. Утім, окрім цілої вимірності, в математиці вже досить давно відоме поняття вимірності нецілої, піонерами в дослідженні якої, до речі, були львівські математики. Практичне ж застосування концепції нецілої вимірності, зокрема в природознавстві, економіці, фінансах і т. д., є відносно недавнім. Його пов’язують з іменем творця фрактальної геометрії Бенуа Мандельброта (1924 – 2010). Ось приклад фракталу – так званий «килим Серпінського», який у 1916 р. вперше описав професор Львівського університету Вацлав Серпінський.

Килим Серпінського: Квадрат розрізають паралельними прямими на дев'ять однакових підквадратів, які утворюють сітку три на три. Центральний квадрат видаляють, а далі цю процедуру повторюють до безмежності для всіх підквадратів, що залишилися. Фрактальна вимірність килима Серпінського df ≈ 1,89.
Яка площа і який периметр цього об'єкта? Його площа дорівнює нулю, адже він являє собою сито: яку б точку я не обрав на його поверхні, попаду в «дірку». При цьому його периметр безмежний, адже якщо б я хотів обійти усі підквадрати, то блукав би по ньому безкінечно. Вимірність об'єкта, площа якого дорівнює нулю, а периметр безкінечності, становить не 1 і не 2, а десь посередині. Можна показати, що для зображеного на рисунку килиму Серпінського вона рівна df = ln8/ln3 ≈ 1,89. Об'єкти, які мають нецілу вимірність і володіють певними характерними властивостями, зокрема властивістю самоподібності (подібні самі до себе на різних масштабах), називаються фракталами (від лат. fractus – поламаний). Уявімо собі ламану лінію, яка сама себе не перетинає. Якщо її повороти уявити дуже густими, то вона, залишаючись лінією, починає нагадувати площину. Вимірність такого об'єкта не 1 (як у лінії) і не 2 (як в площини), а також знаходиться десь посередині. Приклад такої лінії із нецілою вимірністю – траєкторія блукання із самоуниканням (self avoiding walk). Розглянемо наступну задачу: стоїть п'яниця, тримається за стовп і робить певну кількість кроків. Як далеко він відійде від стовпа? Оскільки п'яниця постійно заточується, він не йде рівно, а робить кожен наступний крок у випадковому напрямку: його траєкторія є випадковим блуканням (random walk). Можна показати, що середній характерний розмір такого блукання дорівнює квадратному кореню від зробленої кількості кроків. Тобто якщо він зробив сто кроків (N=100), то від стовпа відійшов приблизно на десять (R≈10): N~R² . Відповідно, вимірність такого об'єкту становить df =2. Якщо при такому випадковому блуканні на площині ще й накласти умову, що траєкторія не може перетинати сама себе (блукання із самоуниканням), то можна показати, що відповідна вимірність становить df =⁴/₃.
Я навів усі ці приклади для того, щоб тепер подивитися на місто, як на об'єкт з нецілою вимірністю. Розгляньмо, наприклад, одну із структур міста – мережу його громадського транспорту. На рисунку, поданому нижче, показана залежність характерного розміру маршрутів громадського транспорту R від кількості зупинок N. Якби кожен із маршрутів був прямою лінією, то ця залежність була б лінійна і ми мали б спостерігати співвідношення: N~R. Як бачимо із рисунку, насправді для усередненої відстані лінійною є взаємна залежність логарифмів цих величин ln R ≈ ³/₄ ln N. Це означає, що виконується степеневий закон N~R⁴/₃. Зверніть увагу, що показних степені у цьому законі – нецілий і відповідає фракталу із вимірністю блукання з самоуниканням df =⁴/₃.
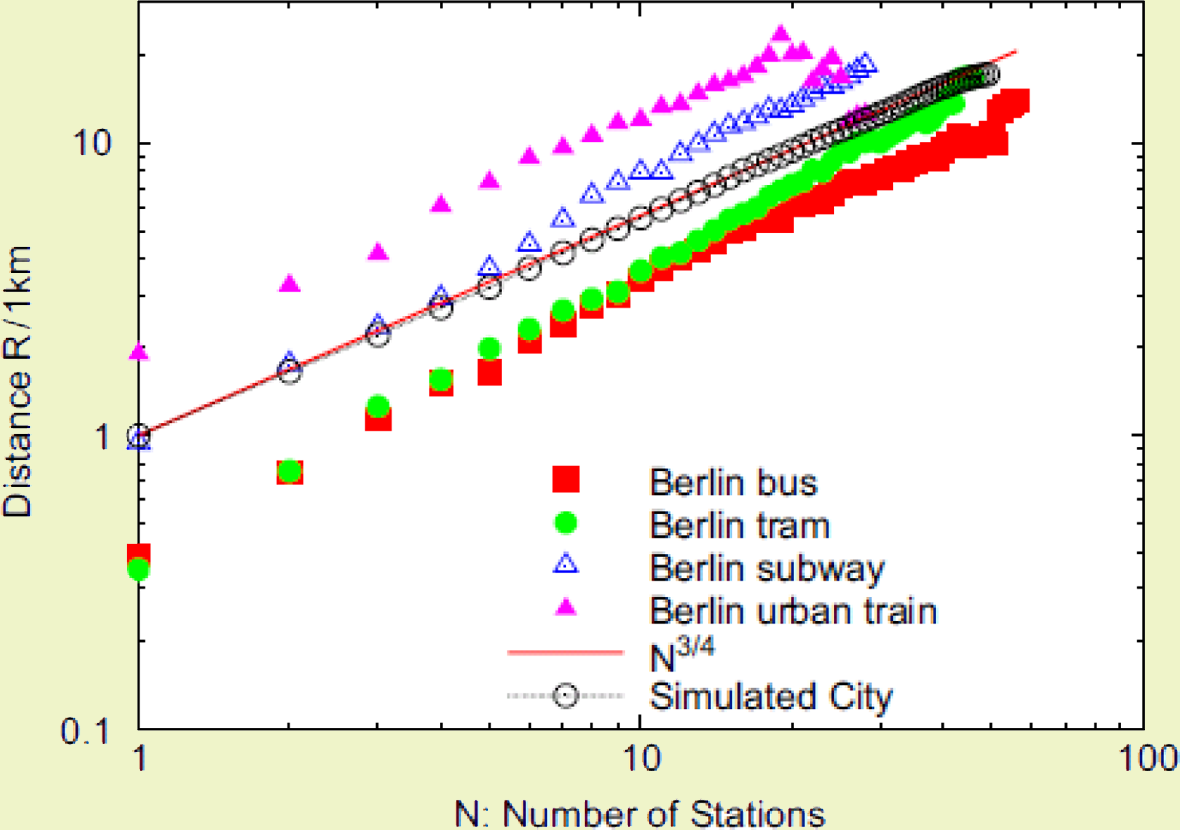
Мандрівки по Берліну, використовуючи різні види громадського транспорту: залежність пройденої відстані R (виміряної у кілометрах від початку до кінця подорожі) від кількості пройдених станцій. Цит. за: C. von Ferber, T. Holovatch,Yu.H.,V. Palchykov. Physica A 380 (2007) 585
Нецілою (фрактальною) вимірністю характеризуються різні міські структури. На малюнку нижче зображена морфологія населення і структура мережі громадського транспорту Лондона.
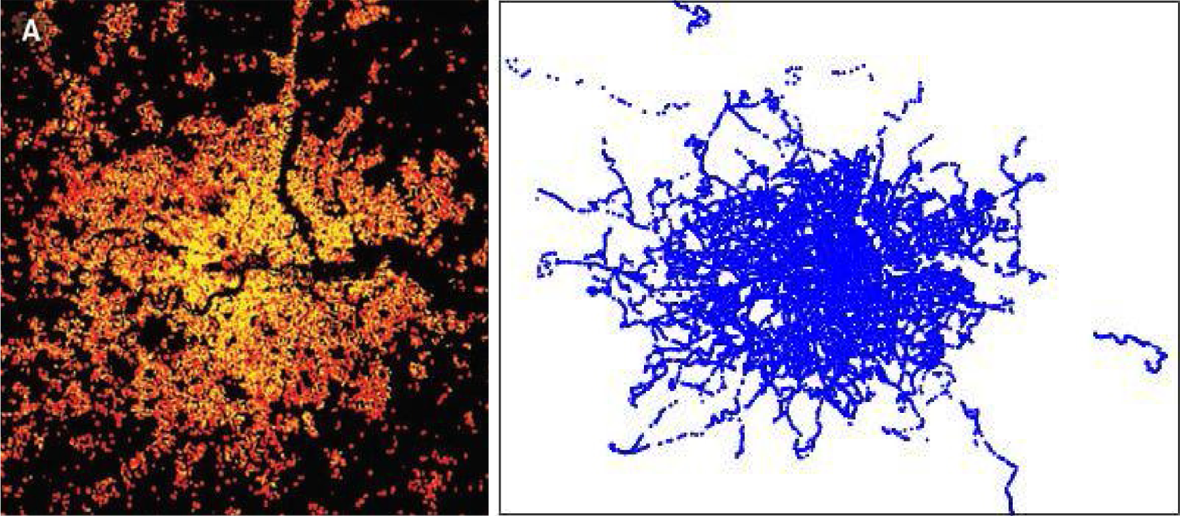
Морфологія населення (зліва) і структура мережі громадського транспорту (справа) великого Лондону. Цит. за: M. Batty, Science 319 (2008) 769; R. de Regt, C. von Ferber, Yu.H., M. Lebovka, unpublished (2016)
Усього мережа громадського транспорту великого Лондону налічує біля 17,000 станцій (кожна з них зображена окремою точкою, які на рисунку справа злилися докупи). Цю мережу також характеризує неціла фрактальна вимірність, яку можна вирахувати. Для цього слід знайти центр маси мережі, оточити його колом, а далі поступово збільшувати радіус цього кола, визначаючи, як зростає у ньому кількість станцій. Якби станції в Лондоні були розподілені рівномірно, то це був би двовимірний об'єкт. Але розподіл станцій нерівномірний. І однією із характеристик цієї нерівномірності є знайдена у такий спосіб неціла (фрактальна) вимірність. У межах проекту аналізу системи громадського транспорту Великої Британії, ми провела подібні розрахунки не тільки для Лондону, але й для інших міст і графств. В усіх випадках між радіусом кола та кількістю станцій виникає степеневий закон із нецілим показником, що дає значення фрактальної вимірності міста. Така залежність виникає не лише для мережі громадського транспорту, але й для багатьох інших характеристик міста і його інфраструктур. Морфологія міста знаходить своє відображення як ієрархія кластерів різного масштабу. – від цілого міста до його окремих структурних одиниць. Таким чином, міста є класичним прикладом фракталів, а їх форма відображає статистичну самоподібність ієрархії кластерів. Часто великі міста зростають за рахунок поглинання менших або за рахунок виникнення і розвитку нових міських центрів на їх границях. Цікаво зазначити, що для глибшого розуміння і опису такого фрактального зростання міст успішно використовуються відомі у фізиці моделі виникнення перколяційного кластеру чи керованої дифузією аґреґації, див. рис. внизу.

Приклади фрактального росту: керована дифузією агрегація (зліва) і перколяція (справа). Цит. за: H. A. Makse, S. Havlin, H.E. Stanley, Nature 377 (1995)
Ці та інші моделі, що використовуються для пояснення фрактального росту міста і його окремих структур базуються та стосовно простих локальних принципах, в наші дні вони успішно застосовуються для опису реальних спостережень і планування розвитку міста. Цікаво, що ці ж моделі використовують для пояснення того, чому неуспішними в минулому виявилися спроби ввести правила побудови ідеальних міст (таких, наприклад, як італійські ідеальні міста епохи Відродження).
Наступний пункт, якого я хотів би торкнутися, можна метафорично назвати «життям міста». Традиція уявляти місто як живий організм дуже давня і сягає своїми коренями ще епохи Античності (порівняння античного поліса з живим організмом можна знайти ще в «Політиці» Аристотеля). Сьогодні наш лексикон рясніє порівняннями міста з живим організмом, коли ми, наприклад, кажемо «пульс міста», «ритм міста», «народження чи смерть міста». Проводячи паралель між містом і живим організмом, я хотів би звернути увагу на одну особливість живого, яку також можна відслідкувати і в місті. Ця особливість називається алометричним скейлінгом і полягає, знову ж таки, у виникненні степеневого закону. На рисунку зображено графічну ілюстрацію до т. зв. «закону Клайбера», відкритого ще у 1932 р.
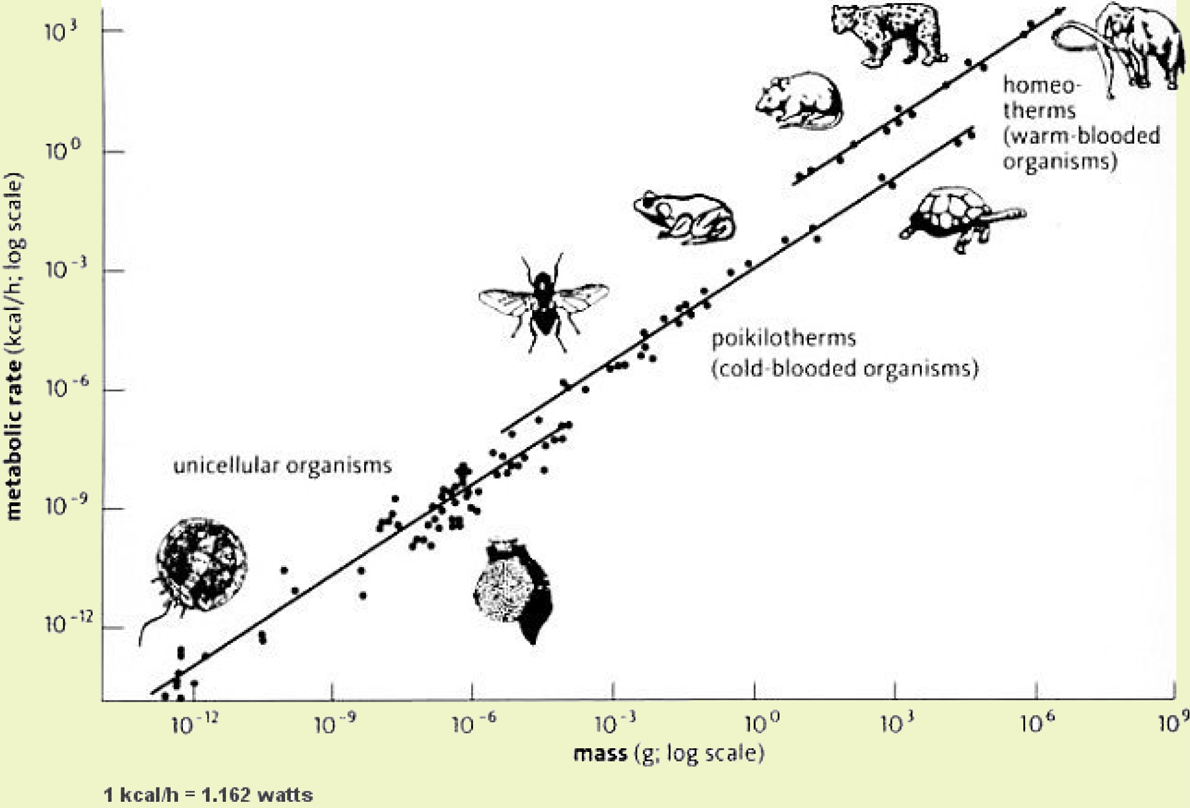
Закон Клайбера пов’язує масу організму (вісь x) із основним обміном речовин (вісь y). Як видно з рисунку, цей закон справджується в діапазоні від 10⁻¹³ до 10⁸ грамів. Цит. за: A Review of the Universe - Structures, Evolutions, Observations, and Theories
Цей закон встановлює залежність між масою тіла організму та швидкістю метаболічних реакцій у ньому. Мова йде про те, скільки потребують енергії для життя живі організми з різною масою. Діаграма представлена на рисунку включає організми різних розмірів і маси – від найлегших одноклітинних (маса 10⁻¹³ грам) до важкого слона (10⁸ грам). Кожен вид показаний крапкою на шкалі. Як видно, усі крапки вишиковуються в подвійному логарифмічному масштабі в струнку пряму, яка свідчить про виникнення степеневого закону. У даному випадку цей закон такий: основний метаболізм B пропорційний до маси M тіла організму у степені ¾: B ~ M¾. Якщо б степінь був «1», то це б значило б, що вдвічі важчий організм потребує вдвічі більше енергії для того, щоб жити (лінійний скейлінг). Тут, однак, показник степеня рівний ¾, це означає, що чим важчий стає організм, тим на одиницю маси йому потрібно менше енергії, щоб вижити, тобто що важчий організм, то ефективніше він використовує енергію (зауважимо, що показник степені у цьому випадку є меншим за 1, або ж скейлінг є сублінійним).
Закон степеневого зв'язку із масою всього організму справедливий і для багатьох інших характеристик живих організмів, наприклад для маси мозку чи діаметру аорти. У цих випадках показник степеня також становить ¾. Коли мова йде про циркуляцію крові чи ріст ембріона, то він дорівнює ¼, а коли про удари серця, то це також ¼, але вже зі знаком «мінус». Важливо, що у всіх цих випадках завжди присутня четвірка й ніколи трійка. Трійку було б легше пояснити, адже ми живемо у тривимірному світі, тож трійка характеризувала б зміну певної величини на кожну одиницю об’єму. Тож чому четвірка? Одне з пояснень полягає в тому, що живі організми містять різноманітні розгалужені мережі – судинну, нервову тощо. Такі мережі не обов’язково мають бути вкладені в трьохвимірний простір: вони можуть відповідати, наприклад, ієрархічній структурі хімічних реакцій чи транспортних процесів, що відбуваються в організмі. Тобто живі організми характеризують три виміри, які пов’язані з об'ємом (ширина, довжина і висота), і присутність мережевих структур, які до закону алометричного скейлінгу додають ще одну одиничку. Тому багато ознак живого характеризує закон, що містить саме четвірку.
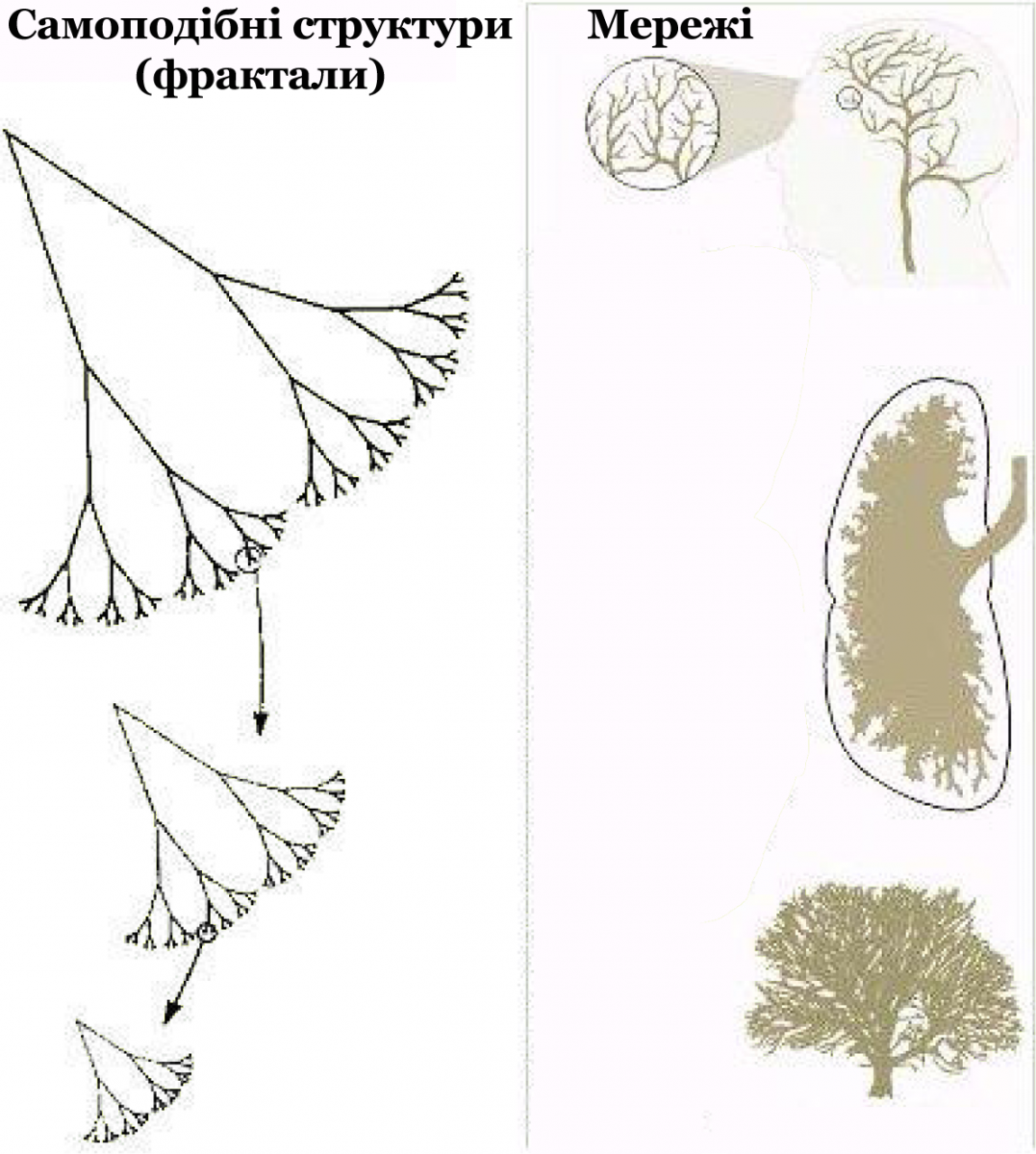
Живі організми характеризують внутрішні фрактальні мережі (зліва), які подані (справа зверху вниз) на прикладі системи кровообігу, будови легенів та розгалуженої структури дерева. Саме ці мережі обумовлюють число «чотири» в алометричному скейлінгу характеристик живих істот. Цит. за: G.B. West, J.H. Brown, B.J. Enquist, Science 284 (1999) 1677
А як же з містами? Подивімось на місто, як на єдиний “організм” і розгляньмо скейлінг його характеристик. Статистичне обчислення цих характеристик спершу зробили для міст в розвинених країнах, але тепер вважають, що ці закони універсальні і діють також у країнах, що розвиваються. Розглянемо спершу такий показник, як сума платні, яку отримують мешканці певного міста — як вона залежить від розміру міста. Зрозуміло, що чим більше місто, тим більше воно заробляє. Залежність суми грошей, яку заробляє місто, від його розміру (кількості мешканців), зображена на рисунку внизу зліва у подвійному логарифмічному масштабі є прямою лінією, що свідчить про існування степеневого закону. За кутом нахилу цієї лінії можна визначити, що показник степеня у цій залежності становить β≈1,12. На рисунку внизу справа зображено іншу характеристику міста - кількісті так званих supercreatives (людей, які створюють інтелектуальний продукт: митців, вчених, літераторів тощо). Їх кількість також зростає степенево залежно із розміром міста, а показник степеня також більший за одиницю (β≈1,15).
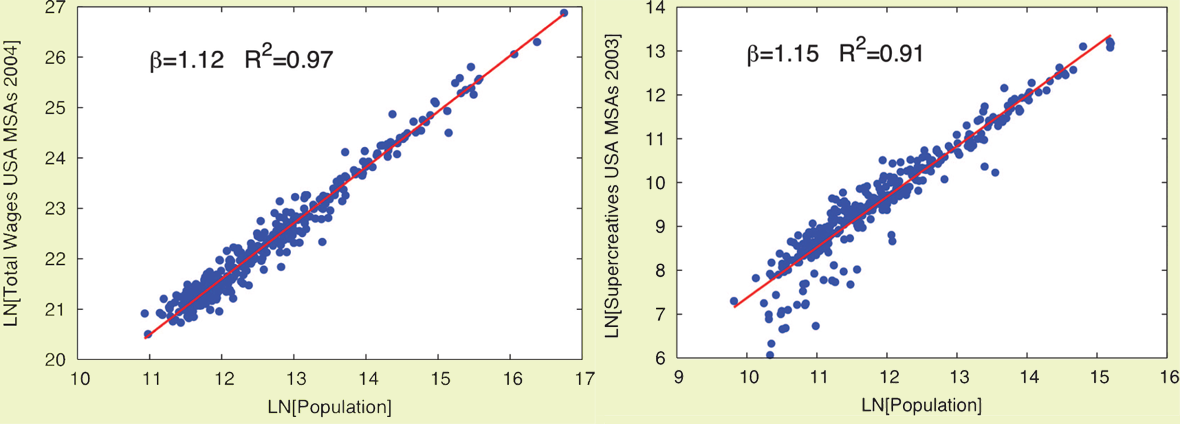
Приклади співвідношень скейлінгу (степеневих законів), що пов’язують соціоекономічні характеристики міст із розміром: сумарна платня (зліва) та кількість supercreatives (справа) у різних містах США. Цит. за: L.M.A. Bettencourt et al. PNAS 104 (2007) 7301
Подібні степеневі залежності характеризують й багато інших соціальних показників, наприклад, кількість патентів, отриманих мешканцями міста (що, певною мірою може служити кількісною оцінкою знань), кількість злочинів чи нових випадків СНІДу, які також зростають пропорційно до розміру міста й з показником степеня >1. В усіх цих випадках важливі не стільки точні значення чисел після коми, а те, що показник степеня більший за одиницю. Тобто скейлінг є суперлінійним. Якби скейлінг був лінійним, тобто показник степеня дорівнював би одиниці, це б означало, що місто з населенням 4 млн. заробляє вдвічі більше чи продукує вдвічі більше знань, ніж місто з населенням у 2 млн. Показник степеня >1 означає, що місто з двічі більшим населенням заробляє чи виробляє знання не в два рази більше, а ще більше за цю величину. Тобто у місті, як в складній системі, виникає додатковий ефект – емерджентність. Однак, такий суперлінійний скейлінг описує лише соціоекономічні характеристики міста. Натомість матеріальні показники міст, що характеризують їх інфраструктуру і нагадують відповідні матеріальні характеристики живих організмів, зростають також пропорційно до розміру міст, але вже з показником степеня < 1: для них, як і для живих організмів, скейлінг є сублінійним. Такі сублінійні закони скейлінгу описують зростання кількості бензозаправок, об’єму продажу пального, довжини мереж електропередачі чи площі поверхні автомобільних доріг, тощо. Тобто у місті з населенням 4 млн. всі ці характеристики будуть не вдвічі більшими, ніж у місті з населенням 2 млн., а менш ніж вдвічі більші. Тут спостерігається аналогія із згаданим вище законом Клайбера: зі зростанням розміру міста, так само як і зі зростанням розміру живого організму, відбувається економія його характеристик.
У цьому контексті важливо наголосити на ще одній концепції, що є однією із основоположних у поведінці складних систем: на універсальності їх поведінки. Не зважаючи на різноманітність міських агломерацій у країнах з різним географічним розташуванням та рівнем економічного розвитку, різною культурною та історичною традицією, виявляється, що зростання соціоекономічних та інфраструктурних характеристик із розміром міст відбувається за одними і тими ж самими універсальними законами. Подібні результати отримані для міських агломерацій США, Китаю, Бразилії та низки інших країн.
Таким чином, зростання інфраструктурних характеристик міст, подібно до зростання характеристик живих організмів, відбувається сублінійно (для міст показник степеня становить β≈0,85 а для живих організмів закон Клайберта передбачає β≈0,75) в той час як зростання соціоекономічних характеристик міст (тобто тих, які не мають аналогів у біології) відбувається за суперлінійним законом. За теорією американського вченого Джефрі Веста (в минулому – президента Інституту Санта Фе у США), якщо система розвивається, підкорюючись законам суперлінійного скейлінгу, то воно рано чи пізно обов'язково зазнає колапсу. Схематично це зображено на наступній ілюстрації. Коли населення міста за певних початкових умов починає рости, то в майбутньому обов'язково настане момент, коли відбудеться його колапс (на ілюстрації цей момент показаний штриховою лінією).
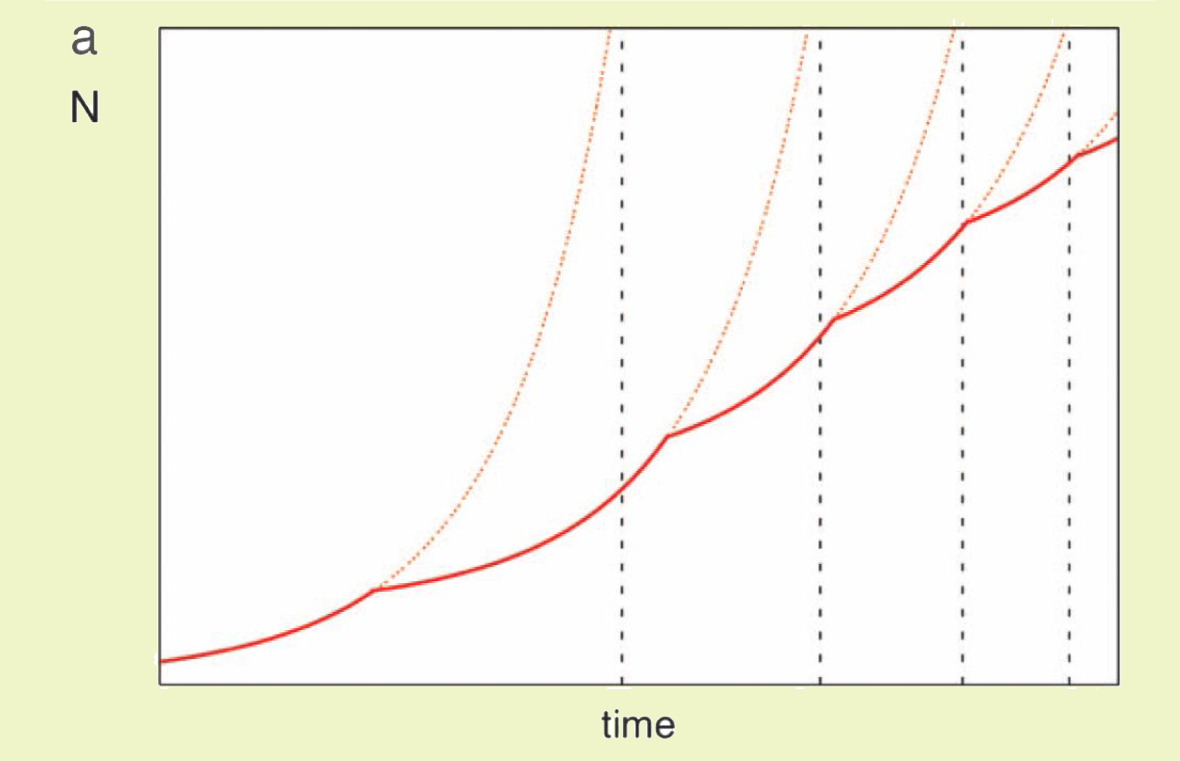
Зміна кількості населення міста (N) з часом. Штриховими лініями показані моменти колапсу, обчислені за заданих початкових умов. Послідовні зміни початкових умов – інновації – змінюють положення колапсу.
Тобто в початкових умовах розвитку міста обов’язково закладена його смерть. Чому ж міста живуть так довго і не помирають? Відповідь на це питання полягає в умовах задачі – «за певних заданих початкових умов». Однак в інфраструктурі міста чи способі життя міста постійно з’являються якісь інновації, наприклад використання бензину чи комп’ютера енергетики (вони можуть бути навіть такими простими, як, наприклад, ідея разом пити каву), які змінюють ці початкові передумови і, отже, збивають на нуль час на годиннику, на якому зафіксована смерть міста. Цикли руху до смерті і її відтермінування через появу інновацій можна побачити на схемі, яка показує темп приросту населення Нью-Йорка з 1800 до 2000 р.

Темп приросту населення Нью-Йорка з 1800 до 2000 р. Вкладений рисунок показує, як зменшується із зростанням населення міста час між послідовними циклами (tc ). Цит. за: L.M.A. Bettencourt et al. PNAS 104 (2007) 7301
Як видно із цієї схеми, зростання населення кожного разу прямувало б до колапсу, однак періоди зростання постійно переривалися періодами спаду. Важливо звернути увагу на те, що від одного циклу до іншого проходить дедалі менше часу. Загальновідомо, що ритм життя прискорюється, але це прискорення можна кількісно виміряти. Так, у сучасній IT індустрії якась стратегічна інновація повинна з’являтися хоча б раз в півроку.
При описі складних систем, коли мова йде про природні чи створені людиною системи, важливу роль відіграє аналіз їх мережевої структури. Як я уже не раз згадував вище, дуже часто саме мережева структура відповідає за функціонування та і за саме виникнення складної системи. Такий аналіз прийнято проводити за допомогою певного математичного апарату, теорії випадкових графів чи, як тепер прийнято казати, теорії складних мереж (complex networks). Я приведу лише один із результатів такого аналізу, проведеного нами для транспортних мереж деяких великих міст. Мережі громадського транспорту - це лише один із прикладів з величезної кількості мереж, що існують в сучасному місті (соціальних мереж різного типу, що пов’язують між собою мешканців міста завдяки їх місцю праці, вподобанням чи сімейним стосункам, технологічних мереж зв’язку, енергопостачання, тощо). Цей підхід розглядає складну систему як сукупність вузлів і зв'язків між ними. Щоб унаочнити цю тезу, уявімо, що кожен з нас – це вузол, який пов’язаний з іншими такими самими вузлами мережею зв'язків (професійних, сімейних, дружніх тощо). Таких соціальних мереж існує дуже багато і вони самі, своєю чергою, також пов’язані між собою. Візьмімо, для прикладу, мережу цитувань. Науковці часто цитують своїх колег, яких особисто знають. Отже, мережа цитувань значною мірою обумовлена мережею знайомств. Такий самий спосіб аналізу, що розглядає певну структуру як сукупність вузлів, пов’язаних між собою сукупністю зв'язків цілком природньо можна застосувати і до аналізу транспортних мереж.
На рисунку нижче зліва схематично показана база даних, яку ми аналізували – це мережі громадського транспорту чотирнадцяти великих міст світу. Діаметр кожного кружечка відповідає кількості населення міста, по осі х подано кількість громадського транспорту у місті, а по осі у – кількість маршрутів. Справа зображено конкретний приклад - частину мережі громадського транспорту Лондону. Подорожуючи в Лондоні, зручно користуватися так званою «Oyster card», якою ви оплачуєте проїзд у транспорті. За допомогою даних про користування такими картками можна відслідкувати всі переміщення пасажирів по місту. Схема нижче показує інтенсивність переміщень по лондонському метро і пасажиропотік кожної лінії. Використовуючи такі дані, досліджують динаміку процесів у мережі транспорту. Я ж приведу деякі дані, що стосуються статичних, незалежних від часу, властивостей мереж, що спричинені їх топологією (тобто тим, як їх вузли поєднані між собою) і географічним розташуванням.
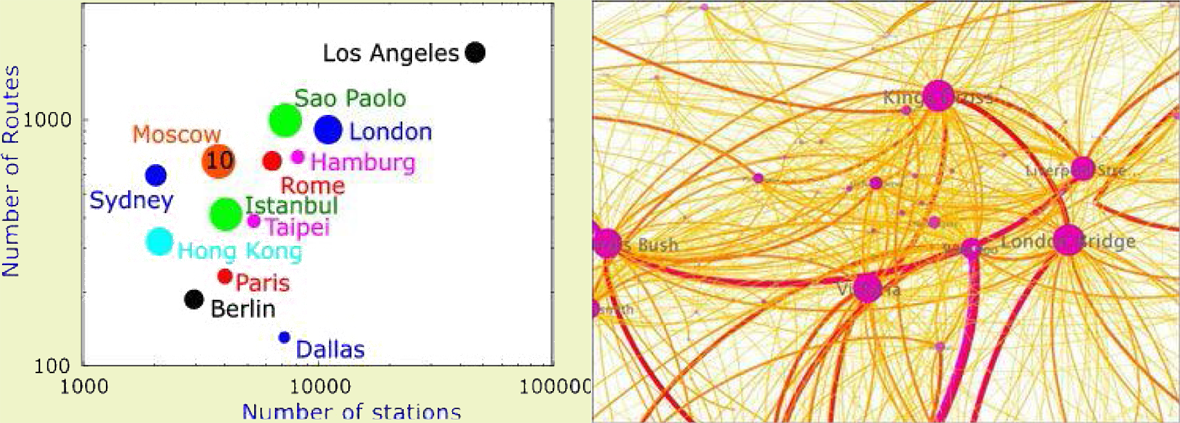
Мережі громадського транспорту великих міст світу використані у нашому аналізі (зліва) та схема переміщень в мережі громадського транспорту Лондону на основі інформації Oyster Card (справа). Цит. за: C. von Ferber, T. Holovatch,Yu.H.,V. Palchykov Eur. Phys. J. B 68 (2009) 261; M. Batty, Science 319 (2008) 769
Говорячи про властивості складних мереж, неможливо оминути увагу таку їх особливість, як стійкість до атак. Атакою називається вилучення якоїсь компоненти мережі, скажімо, для мережі транспорту, це може бути вилучення станції (вузла мережі) чи зв’язку. Особливістю певного класу складних мереж є їх стійкість до випадкових атак: якщо ви вилучите випадковим чином певну кількість її складових частин мережа буде жити далі. «Жити» в тому сенсі, що вона і далі значна частина її вузлів буде зв’язана між собою. Інтернет, наприклад, – це мережа комп’ютерів, які пов’язані між собою через кабель чи антени. Якщо випадково вилучити одну станцію, Інтернет і далі житиме. Виявляється, він існуватиме навіть тоді, коли випадковим чином вилучити 99% усіх вузлів. Таким чином, складна система характерна тим, що вона дуже стійка до випадкових збоїв. Натомість вона дуже вразлива до спрямованих атак, коли викидають не будь-які, а найважливіші вузли. На початку лекції я вже згадував про чутливість складних систем, коли найменші зміни у параметрах можуть привести до кардинальних змін системи як цілого.
На рисунку внизу ці два ефекти – стійкість до випадкових збоїв і вразливість до спрямованих атак – продемонстровано на прикладі реакції мереж громадського транспорту різних міст до вилучення їх станцій.
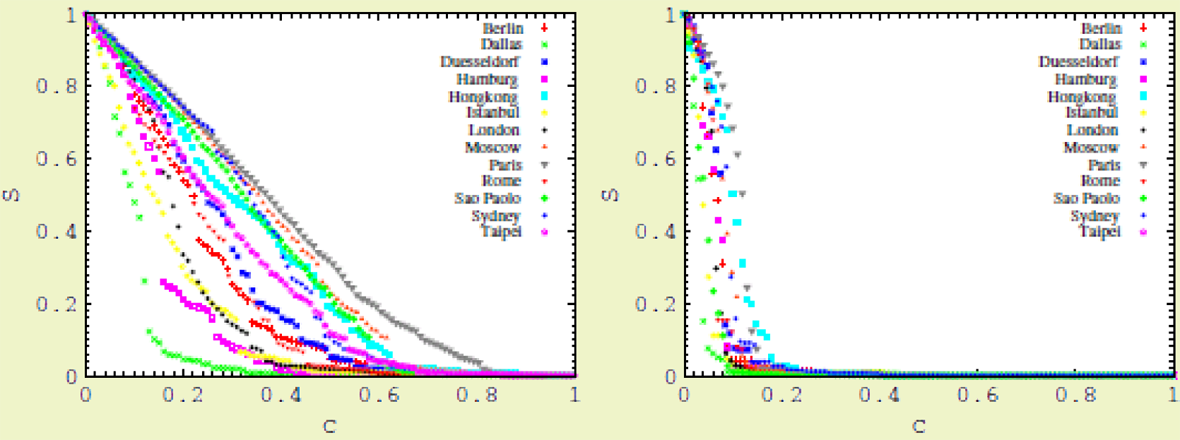
Розмір найбільшої зв’язної компоненти S мереж громадського транспорту різних міст світу як функція частки вилучених станцій c для атак, проведених за різними сценаріями. Зліва – випадкова атака (станції вилучаються випадковим чином). Справа – спрямована атака (спочатку вилучаються габи – стації із найбільшою кількістю зв'язків). Цит. за: B.Berche, C. von Ferber, T. Holovatch, Yu.H., Adv. Complex Syst. 15 (2012) 1250063
У проведеному нами моделюванні досліджувалося, як змінюється розмір найбільшої зв’язної компоненти мережі (S) при послідовному вилученні із неї станції громадського транспорту (частка вилучених станції – с). Таке вилучення моделювалося на комп’ютері за різними сценаріями. За випадковим сценарієм, станції вилучалися цілком випадковим чином (рисунок зліва). При спрямованих атаках, спершу усувалися найважливіші станції. Відразу зазначу, що такі найважливіші станції не обов’язково повинні бути габами – наші обчислення дозволяють виявити різні характеристики ‘важливості’, які часто виявляються далеко не очевидними. Тим не менше, на рисунку справа показано результат вилучення із мережі станцій із найбільшою кількістю вузлів. Як видно із порівняння рисунків, реакція мереж на атаки проведені за різними сценаріями суттєво відрізняється. Так, мережа транспорту Парижу рівномірно зменшується при випадкових атаках – це свідчення її стійкості до випадкових збоїв. Однак досить змінити сценарій атак і вилучення порівняно невеликої частки її станцій (~ 5 %) приводить до кардинального зменшення розміру мережі (див. рис. вгорі справа).
Останнє, на чому я хотів би зупинити увагу, – це мобільність і система комунікацій у місті. Розгляньмо переміщення людей в місті. Кожен з нас переміщається по місту індивідуально, але коли ми розглянемо переміщення людей загалом, то виявляється, що і тут присутній ефект виникнення (емерджентності) певних колективних закономірностей. Є ціла низка причин, чому важливо знати ці закономірності. Це і планування міського дизайну і прогнозування і запобігання корків на дорогах, і зменшення розповсюдження інфекційних захворювань, і планування дій у надзвичайних ситуаціях, тощо. Задача визначення закономірностей руху населення шляхом прямого вимірювання є складною, вона вимагає значних технічних, організаційних, а, отже, і фінансових затрат, а також включає в себе питання конфіденційності. Тому особливо цікавим і перспективним є пошук моделей, які б дозволили передбачити рух населення на основі інших спостережуваних даних. Деякі з таких моделей базуються на так званому «законі гравітації». Як ми знаємо ще зі школи, класичний закон гравітації (Ньютонів закон всесвітнього тяжіння) стверджує, що сила притягання між двома тілами прямо пропорційна до їх мас, m₁ і m₂ і обернено пропорційна квадрату відстані між ними, (d₁₂)². Щось подібне спостерігається і в місті, коли ми аналізуємо те, як люди переміщаються і як вони спілкуються.
Дослідження, яке провів співробітник ІФКС НАН України Василь Пальчиков у співпраці з колегами з інших установ, було основане на аналізі великої бази даних оператора мобільного зв'язку Orange для країни Кот д'Івуар (83% населення цієї країни мають мобільні телефони). Мобільність населення відстежувалась на основі аналізу переміщення абонентів між баштами стільникового зв'язку. Зокрема, досліджували масив спілкування забезпеченого протягом п'яти місяців сервісом 1231 башти. Крім того, протягом двох тижнів відслідковувалися дзвінки та переміщення між баштами 50 тис. випадково обраних абонентів. Загалом це дослідження охопило 143 міста а база даних налічувала 64 млн. дзвінків. Отримані у ньому результати стверджують: якщо відомо, скільки людей живуть в ділянках, охопленій покриттям башт, то можна передбачити, як вони переміщатимуться між ними. І це передбачення описується «законом гравітації»: мобільність (кількість переміщень) mᵢⱼ населення між ділянками, що обслуговуються баштами стільникового зв'язку i і j прямо пропорційна до кількості населення, що проживає в межах башт, Nᵢ і Nⱼ і обернено пропорційна до певної степені γ відстані між ними, (d₁₂)ᵞ. Подібний закон (але вже з іншим показником степені δ описує зв'язок кількості телефонних розмов cᵢⱼ між ділянками, що обслуговуються баштами стільникового зв'язку i і j. Ця величина прямо пропорційна до кількості населення, що проживає в межах башт, Nᵢ і Nⱼ і обернено пропорційна до відстані між ними, (d₁₂)ᵟ. Дію цих законів продемонстровано на рисунку внизу.
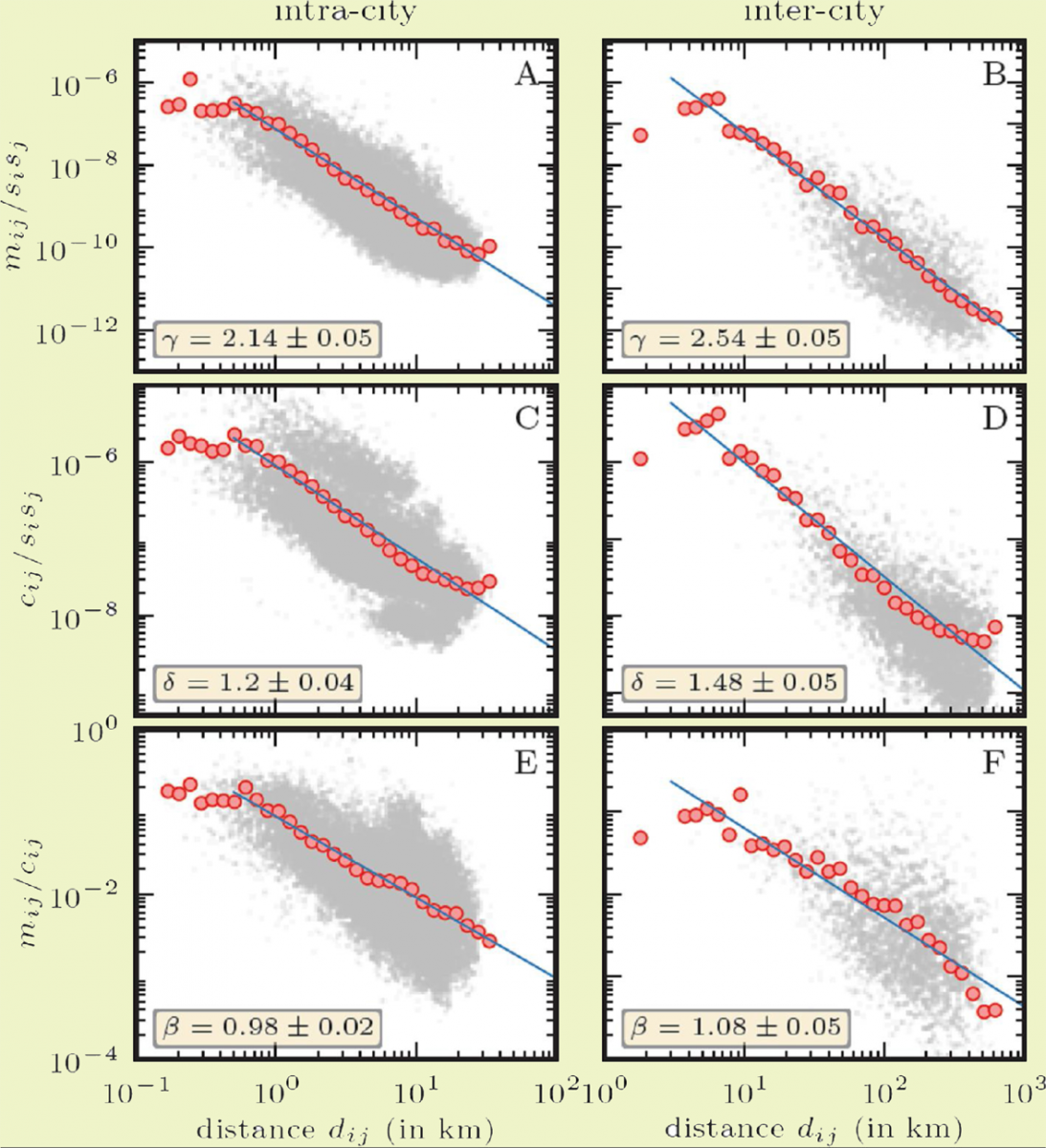
Закон «соціальної гравітації»: кількість переміщень mij і кількість телефонних розмов cij між баштами мобільного зв’язку і і j пропорційна населенню, що проживає в їх межах, та обернено пропорційна відстані між ними. Цит. за: V. Palchykov et al. Scientific Reports 4 (2014) 6174
Виявляється, що те, як люди телефонують, і те, як вони переміщуються, підлягає дії степеневих законів, із, знову ж таки, універсальними (незалежними від деталей системи) показниками степеня: вступає в дію закон гравітації – не всесвітнього тяжіння, а «соціальної гравітації» людей в межах міста. Чому люди їздять і дзвонять – це вже запитання не до фізиків, але саме завдяки фізикам, які займаються складними системами, ми знаємо про цю кореляцію і цей закон.
У своїй доповіді я говорив про міста як про складні системи. Як згадувалось на початку, непросто з погляду частинки уявити і зрозуміти поведінку цілого: more is different! Згадаю ще слова Аристотеля, що ціле – це більше, ніж сума його частин. Я намагався продемонструвати, як концептуальний апарат статистичної фізики дозволяє подивитися на поведінку міста у формалізмі науки про складні системи, що вивчає системи багатьох взаємодіючих агентів і аналізує процеси адаптації взаємодій, самоорганізації, виникнення степеневих законів, стійкості утворених структур. Теорії, що описують функціонування міста, як складної системи, ще лише формуються. Але, як вважають багато із наших сучасників, за ними – майбутнє. Адже, як сказав Стівен Гокінґ ще в минулому столітті – I think the next century will be the century of complexity!
Лекція в рамках семінару "Обрії науки" (17.11.2016, в приміщенні Українського католицького університету).
Занотував Євген Ланюк.
17.01.2017