Про математику. Від основ до незбагненного.

Понад дві з половиною тисячі років математики були перейняті розв'язуванням рівняння відносно х. Історія їхніх спроб знайти «корені» — розв'язки — щораз складніших рівнянь є однією з великих епопей в історії людського мислення.
Утім існувала дражлива дрібна зачіпка, яка не розсмокчеться: розв'язки часто містять квадратні корені від'ємних чисел. Такі розв'язки довший час висміювали як «софістські» чи «надумані», тому що вони здавалися явно абсурдними.
Приблизно до 1700 року математики вірили, що квадратних коренів від'ємних чисел попросту не існує.
Адже вони не могли бути додатними числами, оскільки добуток двох додатних чисел завжди є додатним, а ми шукаємо числа, квадрат яких є від'ємним. Також не підходять від'ємні числа, оскільки добуток двох від'ємних чисел знову ж таки є додатним. Здавалося, нема надії знайти числа, які, помножені самі на себе, давали б від'ємні числа.
Ми вже стикалися з подібними кризами раніше. Вони трапляються щоразу, коли наявні операції заходять задалеко, туди, де вони вже не здаються сенсовними. Так само, як результатом віднімання більших чисел від менших стала поява від'ємних чисел, а ділення породило звичайні і десяткові дроби, довільне застосування квадратних коренів врешті-решт змусило числовий універсум розширюватись… знову.
Історично цей крок був найболючішим зі всіх. Квадратний корінь з -1 досі має принизливе ім'я і, ця курвалькувата літера служить постійним нагадуванням про його «уявний» статус.
Цей новий різновид числа (якщо ви волієте залишатись агностиком, називайте його символом, а не числом) є означений за допомогою властивості
i² = –1.
Щоправда, i неможливо знайти десь на числовій прямій. З цього погляду воно є набагато незвичайнішим, ніж нуль, від'ємні числа, дроби чи навіть ірраціональні числа, бо всі вони — хоч би якими дивними були — мають своє місце на прямій.
Але якщо не бракує уяви, у наших мізках знайдеться місце й для і. Воно живе поза числовою прямою, під прямим кутом до неї, на своїй власній уявній осі. І коли ви з'єднаєте цю уявну вісь зі звичайною «дійсною» числовою прямою, ви утворите двовимірний (2D) простір — площину, де живуть нові різновиди чисел.

Йдеться про «комплексні числа». Тут комплексний не означає складний, а означає, що два типи чисел, дійсне і уявне, складені, щоб утворити комплекс — гібридне число на зразок 2 + 3i.
Комплексні числа є дивовижними, це апогей числових систем. Вони мають всі ті самі властивості, що й дійсні числа, їх можна додавати і віднімати, множити і ділити, але вони є кращими, ніж дійсні числа, тому що вони завжди містять корені. Ви можете взяти квадратний корінь, чи кубічний корінь, чи будь-який корінь з комплексного числа, і результат однаково буде комплексним числом.
Навіть краще: велике твердження, що зветься основною теоремою алгебри, каже, що корені будь-якого многочлена завжди є комплексними числами. У цьому сенсі вони є кінцем пошуків, заповітною метою. Вони є кульмінацією мандрівки, яка почалася з 1.
Ви зможете оцінити практичну цінність комплексних чисел (або визнати її можливою), якщо зумієте їх візуалізувати. Ключем до цього є зрозуміти, як виглядає множення на і.
Припустимо, ми множимо довільне додатне число, скажімо 3, на і. Результатом є уявне число 3і.

Отож множення на і виконує поворот на квадранс проти годинникової стрілки. Воно бере стрілку завдовжки 3, яка вказує на схід, і перетворює її в нову стрілку такої самої довжини, яка тепер показує на північ.
Саме з цієї причини комплексні числа люблять інженери-електрики. Такий компактний спосіб вираження поворотів на 90 градусів є дуже зручним для них, коли вони працюють зі змінними струмами і напругами, чи електричними і магнітними полями, оскільки ті часто викликають коливання чи хвилі, зсунуті по фазі на чверть циклу (тобто 90 градусів).
Насправді комплексні числа незамінні для всіх інженерів. В аерокосмічній інженерії вони спростили перший розрахунок підіймальної сили крила літака. Цивільні інженери та інженери-механіки постійно використовують їх для аналізу вібрацій надземних пішохідних переходів, хмарочосів та автівок на розбитих шляхах.
Властивість повороту на 90 градусів також проливає світло на те, що насправді означає i² = –1. Якщо ми помножимо додатне число на i², відповідна стрілка повернеться на 180 градусів, перекинувшись зі сходу на захід, тому що два повороти на 90 градусів (по одному на кожен множник і) разом дають поворот на 180 градусів.
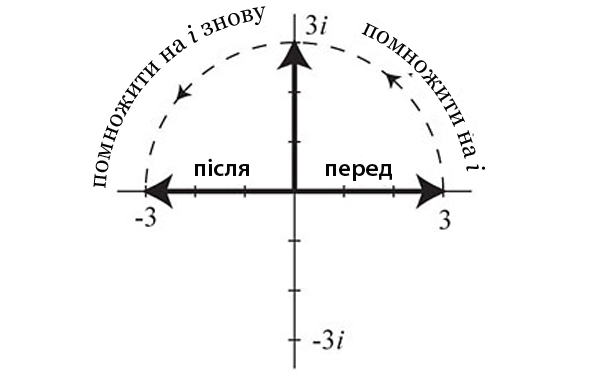
Але множення на -1 виконує точно такий самий поворот на 180 градусів. В цьому сенсі i² = –1.
Комп'ютери вдихнули нове життя в комплексні числа й одвічну проблему знаходження коренів. Машини на вашому столі — коли вони вільні від інтернет-навіґації чи електронного листування — здатні відкривати речі, про які античні мислителі навіть не могли мріяти.
В 1976 р. мій колеґа з Корнелльського університету Джон Габбард почав вивчати динаміку Ньютонівського методу, потужного алгоритму для знаходження коренів рівнянь на комплексній площині. Цей метод вибирає початкову точку (наближення до кореня) і робить певні обчислення, які його поліпшують. Роблячи це знову і знову і завжди використовуючи попередню точку, щоб отримати ліпшу, цей метод сам розраховує свої наступні кроки і швидко фокусується на корені.
Габбард зацікавився проблемами з багатьма коренями. В такому разі, який корінь знайде цей метод? Він довів, що коли коренів є лише два, то ближчий завжди виграє. Але наявність трьох чи більше коренів збивала його з пантелику. Його попереднє доведення вже не спрацьовувало.
Тоді Габбард зробив експеримент. Чисельний експеримент.
Він запрограмував комп'ютер виконувати метод Ньютона, маркуючи різними кольорами мільйони різних початкових точок залежно від того, до якого кореня вони наближаються, і зменшуючи насиченість забарвлення цих точок відповідно до того, як швидко вони туди дістаються.
Перед тим як глянути на результат, він передбачив, що корені найшвидше притягуватимуть близькі точки і тому вони мають проявитися як світлі плями в суцільних кольорових клаптях. Та що діється на межах між цими клаптями? Цього він не міг би обрисувати, принаймні не в своїй уяві.
Відповідь комп'ютера вражала.

Межі виглядали як психоделічні галюцинації. Кольори перемішувалися у майже неймовірно безладний спосіб, дотикаючись один одного в нескінченно великій кількості точок і завжди троїсто. Іншими словами, хай би де стикалися два кольори, завжди з'являвся третій і приєднувався до них.
Збільшення меж виявило візерунки всередині візерунків.

Структура була «фракталом» — складною фіґурою, чия внутрішня структура повторювалася у все дрібнішому і дрібнішому масштабі, як показано у цьому неперервному панкратичному збільшенні:
Ба більше: поблизу межі панував хаос. Дві точки могли стартувати дуже близько одна від одної, якийсь час стрибати пліч-о-пліч, а потім розбігтися до різних коренів. Передбачити, який корінь переможе, було неможливо, як і в грі в рулетку. Щось незначне — крихітні, невідчутні зміни у початкових умовах — може все змінити.
Праця Габбарда була ранньою спробою того, що зараз називається «комплексною динамікою», яскравою сумішшю теорії хаосу, комплексного аналізу і фрактальної геометрії. У певному сенсі вона повернула геометрію до її коренів. У 600 р. до н.е. написаний санскритом посібник для будівничих храму в Індії подав детальну геометричну інструкцію для обчислення квадратних коренів, потрібних для проектування ритуальних вівтарів. Через понад дві з половиною тисячі років математики усе ще шукали корені, але тепер інструкції були написані бінарним кодом.
Деяких уявних друзів ви не позбудетеся ніколи.
Steven Strogatz
The Joy of X
Зреферувала Галина Грабовська
09.09.2016
